 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Фазовая плоскость
Пусть заданы уравнения системы второго порядка
| (5.2) |
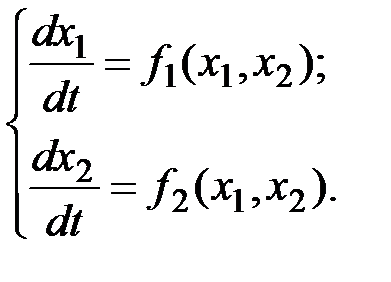
Фазовую траекторию в этом случае можно получить путем деления второго уравнения системы (5.2) на первое
| (5.3) |

и решения полученного дифференциального уравнения 1-го порядка при конкретных начальных условиях.
Если функции f 1 и f 2 однозначны, то каждой точке (х 1, х 2) соответствует единственное значение производной dx 2/ dx 1 (наклона касательной к фазовой траектории), т. е. через эту точку фазовой плоскости проходит только одна фазовая траектория. Единственность нарушается в так называемых особых точках, соответствующих состояниям равновесия системы
| (5.4) |

Координаты особых точек определяются из уравнений
| (5.5) |
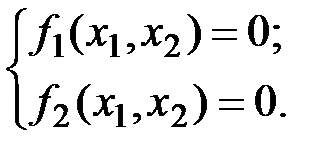
В особых точках имеется неопределенность производной dx 2/ dx 1 = 0/0. Каждая особая точка изображает отдельное (тривиальное) решение системы (5.2) и должна рассматриваться как отдельная фазовая траектория.
В качестве фазовой переменной x 1 часто выбирается переменная входа нелинейного элемента, а в качестве x 2 – ее производная. В этом случае система уравнений (5.2) принимает вид:
| (5.6) |

| (5.7) |

Тот факт, что х 2 = dх 1/ dt, придает фазовой плоскости следующие свойства:
· особые точки располагаются только на оси абсцисс, где
х 2 = dх 1/ dt = 0;
· в верхней полуплоскости (х 2 = dх 1/ dt > 0) фазовые траектории направлены слева направо, т. е. в сторону увеличения х 1, а в нижней полуплоскости ― справа налево;
· фазовые траектории ортогональны оси абсцисс, так как при х 2 = 0 имеем dх 2/ dх 1 = ¥.
Поиск по сайту: