Метод гармонического баланса

Проблема существования автоколебаний и оценки их размаха является крайне сложной и не имеет строгого математического решения. Однако существует простой подход, дающий разумные приближенные результаты – метод гармонического баланса (гармонической линеаризации), предложенный Н.М. Крыловым[3] и Н.Н. Боголюбовым.

Рассмотрим систему с одним нелинейным статическим элементом (рис. 5.24) с однозначной нечетной характеристикой (без гистерезисной петли).

Рис. 5.24. Система с одним нелинейным элементом

Получим уравнение системы относительно ошибки e (t):

e (t) + G (p) z (t) = 0; z (t) = Ф[ e (t)].

Будем искать колебательное решение в виде гармонической функции e (t) = asin w t и подберем амплитуду a и частоту w, чтобы уравнения системы удовлетворялись тождественно.

Так как функция Ф[ e (t)] является нечетной, то ее разложение в ряд Фурье имеет вид

где z_k – коэффициенты ряда Фурье; для нечетной функции

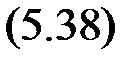
Коэффициенты z_k зависят только от вида нелинейной функции Ф[ e ] и амплитуды a.

Учтем только одно слагаемое в разложении, принимая z (t)= z ₁sinw t. Получим условия для определения a и w.

e (t) + G (p) z (t) = 0, e (t) = a sinw t, z (t) = z ₁sinw t Þ

a sinw t + G (p) z ₁sinw t = 0 Þ

a sinw t + z ₁[| G (i w)|sin(w t + arg(G (i w)]=

a sinw t+ z ₁| G (i w)|[sinw t cosj + cos w tsin j] =

asin w t + z ₁[ U (w) sin w t + V (w) cos w t ] =0 Þ

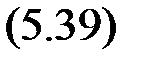z ₁ V (w) = 0, a + z ₁ U (w) = 0,

где V (w) = Im G (i w), U (w) = Re G(i w).

Условия z ₁ V (w) = 0, a+ z ₁ U (w) = 0 можно записать в виде одного соотношения|

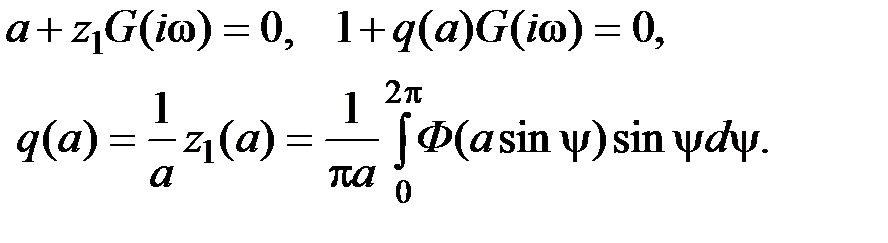
Это основное уравнение метода гармонического баланса. Функция q (a) называется коэффициентом гармонической линеаризации. Поясним смысл слов «гармонический баланс» и «гармоническая линеаризация».

Приняв e (t) = a sinw t, z (t) = z ₁sinw t, мы удовлетворили уравнения системы, отбросив в соотношении z =Ф[ e ] все слагаемые ряда Фурье, кроме первой гармоники, т. е. сбалансировали в уравнении системы гармоники вида sinw t.

С другой стороны, этот прием эквивалентен предположению, что

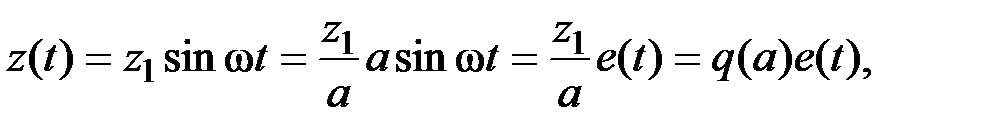
т. е. выход z (t) и вход e (t) нелинейного элемента связаны линейной зависимостью с коэффициентом пропорциональности q (a). Замена нелинейного элемента линейным элементом, коэффициент усиления которого зависит от амплитуды входа, именуется гармонической линеаризацией нелинейности. Прием гармонического баланса эквивалентен гармонической линеаризации, если этот коэффициент принят равным

Подставляя z = q (a)∙ e в уравнение e (t) + G (p) z (t) = 0, получим

[1+ q (a) G (p)] e (t)=0.

Тогда основное соотношение гармонического баланса
1+ q (a) G (i w) = 0 может интерпретироваться как условие наличия чисто мнимого корня у характеристического уравнения гармонически линеаризованной системы.

Подчеркнем, что коэффициент q (a) гармонической линеаризации зависит от амплитуды a, которая заранее неизвестна, и в этом принципиальное отличие уравнения [1+ q (a) G (p)] e (t) = 0 от обычного линейного уравнения.

Как мы уже говорили, коэффициент гармонической линеаризации q (a) можно найти в явном виде, вычисляя соответствующий интеграл. При известной функции q (a) определение величин a и w удобно произвести графоаналитически. Для этого есть несколько вариантов.

Вариант 1 (рис. 5.25).

· построить график V (w) и найти w = w* > 0, при которой V (w*) = 0. Значение w* определяет частоту автоколебаний (период автоколебаний T = 2p/w*);

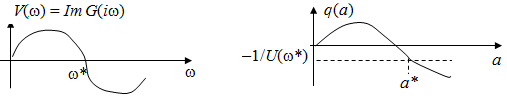
Рис. 5.25. Графическое определение параметров автоколебаний

· построить график q (a) и найти точку его пересечения с прямой, проведенной параллельно оси абсцисс на уровне –1/ U (w*). Эта точка определяет амплитуду автоколебаний a*.

Вариант 2 (диаграмма Гольдфарба, рис. 5.26).

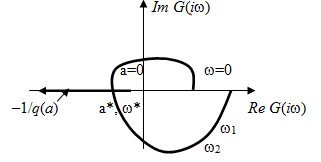
Рис. 5.26. Диаграмма Гольдфарба

· построить годограф G (i w), разметив точки на кривой соответствующими значениями частоты w Î [0, ¥);

· на вещественной оси расположить годограф функции –1/ q (a), т. е. вычислить значения этой функции при a Î [0, ¥);

· точка пересечения графиков дает решение a * на годографе –1/ q (a) и w* на годографе G (i w).

Вариант 3 (диаграмма Айзермана, рис. 5.27).

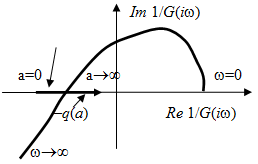
Рис. 5.27. Диаграмма Айзермана

· построить годограф G ^-1(i w);

· построить годограф функции – q (a);

· точка пересечения годографов дает решение a *, w*.

Все эти варианты следуют из соотношения 1 + q (a) G (i w) = 0:

V = Im G (i w) = 0, q (a) = – U ^-1 = –[Re G (i w)]^-1 Þ G (i w) = –1/ q (a) Þ
– q (a) = G ^-1(i w).

Решений может быть несколько, а может не быть ни одного. Если решение существует при каких-либо параметрах системы, то оно будет иметь место и при малых их изменениях, т. е. факт наличия колебаний (колебательный режим) является «грубым».

Пример.

Рассмотрим следящую систему, у которой линейная часть задается передаточной функцией G (p)

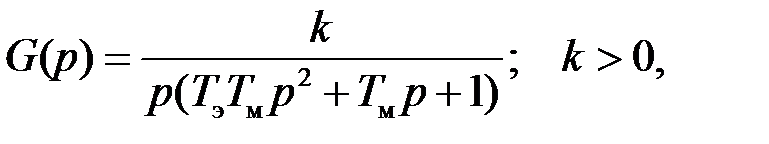
а управление релейное, имеет характеристику «идеального реле»:

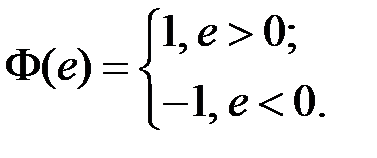
Найдем коэффициент гармонической линеаризации нелинейности q (a) (рис. 5.28).

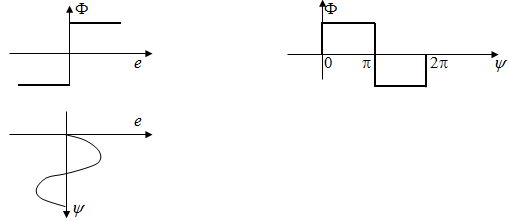
Рис. 5.28. К определению коэффициента гармонической линеаризации

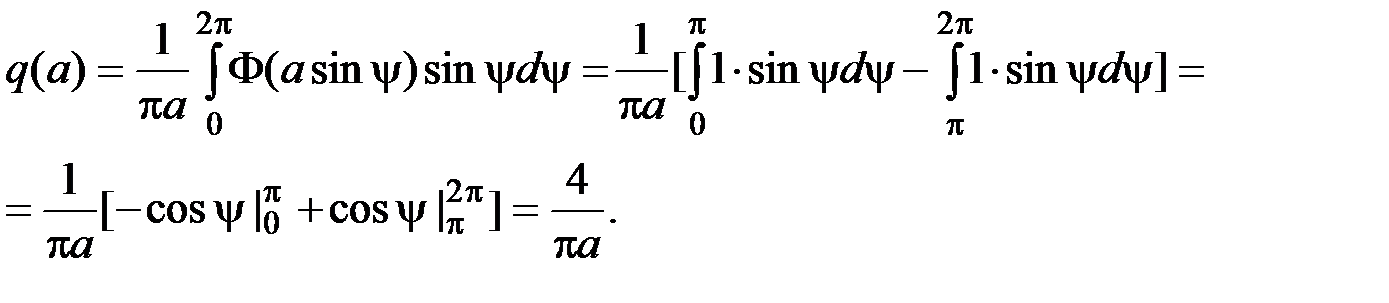
Для аналитического определения параметров автоколебаний используем соотношение G ^-1(i w) = – q (a).

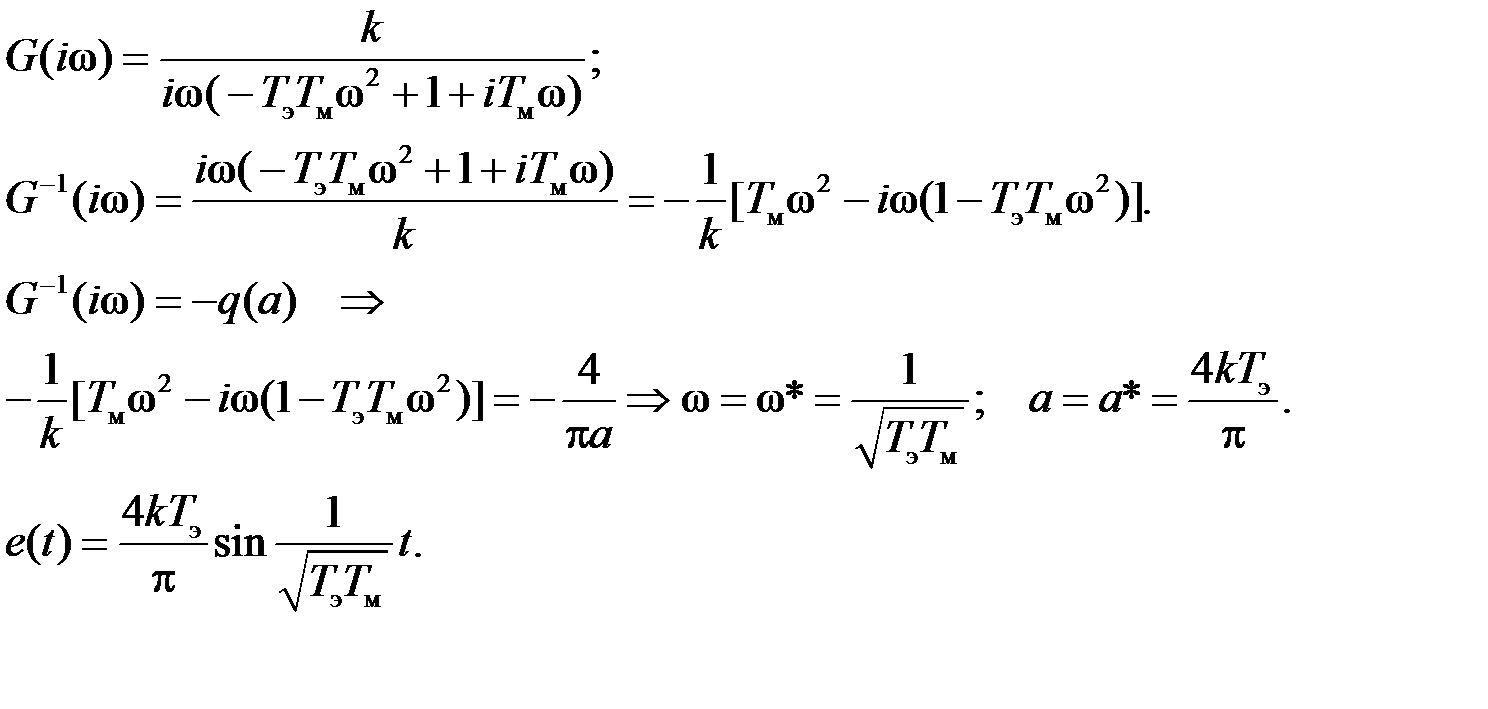
При использовании диаграммы Айзермана (рис. 5.29) имеем:

U ₁ = Re{ G ^-1(i w)}= – Т _мw²/ k, V ₁ = Im{ G ^-1(i w)} = w(1– Т _э Т _мw²)/ k.

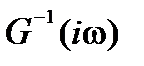
a ®0

a ®¥ U

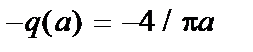a *,w*

Рис. 5.29. Применение диаграммы Айзермана

Теперь получим решение графоаналитическим методом (рис. 5.30):

V (w) = – k (1– Т _э Т _мw²)/w[(1– Т _э Т _мw²)²+ Т _м²w²]; V (w) = 0 Þw * = .

U (w) = – kТ _м / [(1– Т _э Т _мw²)² + Т _м²w²], –1/ U (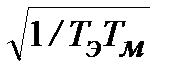) = 1/ kТ _э.

q (a) = 4/p a; 1/ kТ _э = 4/p a Þ a = 4 kТ _э/p.

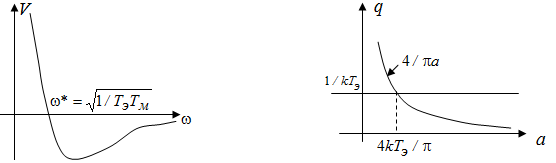
Рис. 5.30. Применение графоаналитического метода

При использовании диаграммы Гольдфарба (рис. 5.31):

U = Re { G (i w)} = – kТ _м / [(1– Т _э Т _мw²)² + Т _м²w²],

V = Im { G (i w)} = – k (1– Т _э Т _мw²) / w[(1– Т _э Т _мw²)² + Т _м²w²].

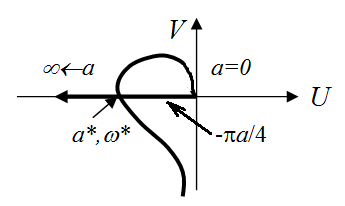
Рис. 5.31. Применение диаграммы Гольдфарба

Замечание 1. Если функция Ф(е) не является нечетной или нарушается условие | G (0)| << | G (i w*)|, основной вариант метода гармонического баланса можно заменить на улучшенный, учитывающий при поиске решения возможную несимметрию колебаний. Решение ищется в виде e (t) = e ₀ + a∙sin w t, где e ₀ – постоянное смещение, а в разложении в ряд Фурье функции z (t) = Ф[ e ₀ + a∙sin w t ] учитывается два слагаемых, т. е. принимается
z (t) = z ₀ + z ₁ ∙ sinw t, где

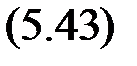
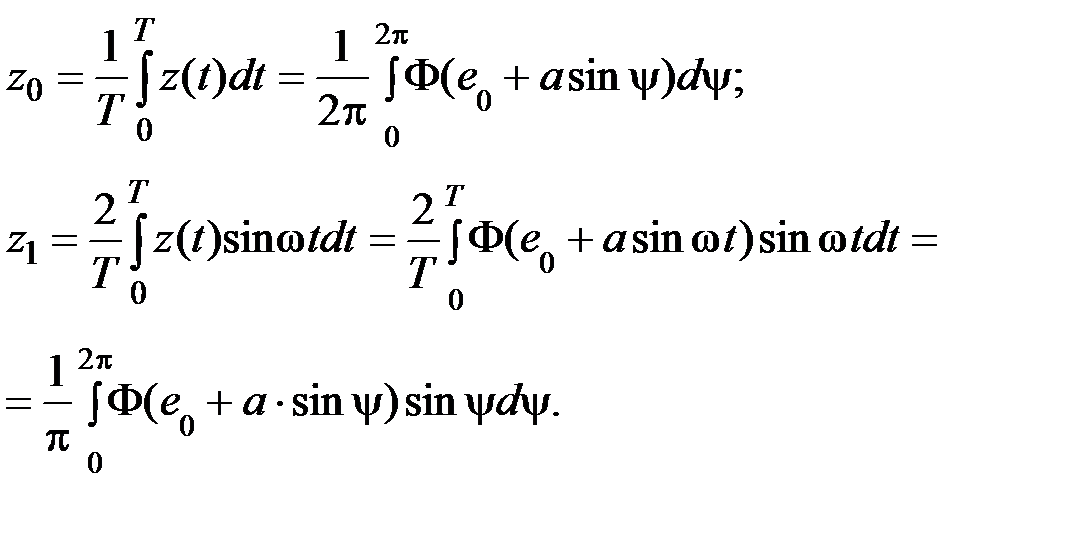
Возможный периодический режим (автоколебания) – решение уравнения e (t) +G (p) z (t) = 0, откуда получаем:

· баланс по постоянной составляющей e ₀ + G (0) z ₀(a,e ₀) = 0,

· баланс по гармонической составляющей (2 уравнения):

а + z ₁(a, e ₀, w) G (i w) = 0.

Имеем 3 уравнения для определения 3-х неизвестных e ₀ *, a*, w *.

Замечание 2. Если функция Ф(е) не является статической однозначной характеристикой (в частности, для нелинейностей типа «люфт»), а также в более общем случае z = Ф(е, 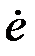), имеем:

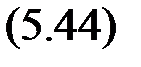
Уравнение гармонического баланса для определения автоколебаний примет вид

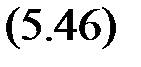G (i w) = –1/ [ q (a) + iq 1(a)].

Пример.

Рассматривается система, линейная часть которой задается передаточной функцией G (р), а нелинейный элемент имеет характеристику люфта.

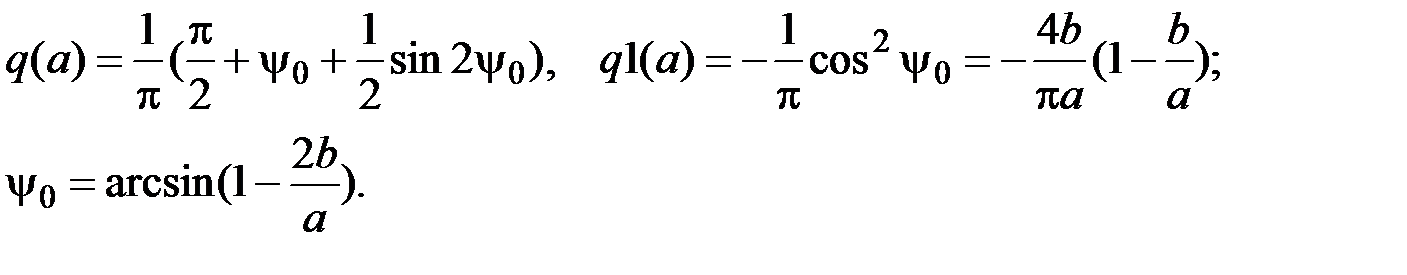
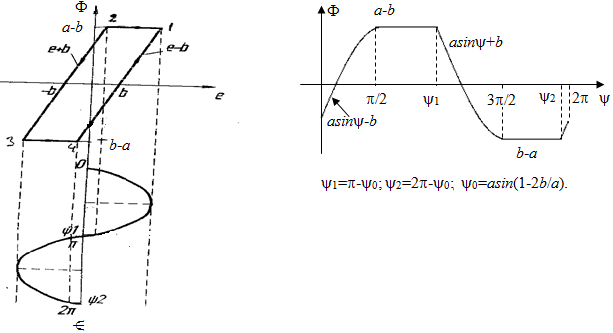
Рис. 5.32. К определению коэффициентов гармонической линеаризации

Далее используем условие G (i w) = –1/ [ q (a) + iq 1(a)] (рис. 5.33).

Рис. 5.33. Применение диаграммы Гольдфарба

Поиск по сайту: