Устойчивость импульсных систем

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

у (n) = С ₁ z ₁ ⁿ + С ₂ z ₂ ⁿ +... + С_mz_mⁿ,

где z _i (i = 1, 2,..., m) – корни характеристического уравнения системы;
С _i – произвольные постоянные, определяемые начальными условиями.

Подобно непрерывным системам, устойчивость линейных импульсных систем автоматического управления определяется по характеристическому уравнению

Q (z) = а ₀ z^m + а ₁ z^{m -1} +...+ а_m = 0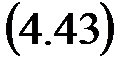

или знаменателю Q (z) передаточной функции G (z) = P (z)/ Q (z) замкнутой системы. Импульсная система устойчива, если все корни характеристического уравнения Q (z) = 0 расположены внутри единичного круга (рис. 4.11), т. е. | z _i| < 1 (i = 1, 2, …, m).

Рис. 4.11. Расположение корней характеристического полинома
устойчивой импульсной системы

Несмотря на наличие дискретных аналогов всех критериев устойчивости непрерывных систем, простейший способ выяснения устойчивости дискретной системы состоит в использовании в характеристическом уравнении Q (z) = 0 или в передаточной функции G (z) подстановки z = (w +1)/(1– w) с последующим применением известных критериев устойчивости непрерывных систем.

Указанная подстановка замечательна тем, что переводит внутренность единичного круга плоскости z в левую полуплоскость w. Действительно, для внутренности единичного круга имеем | z | < 1. Тогда при w = a + ib, где a = Re w, b = Im w получим из этого условия:

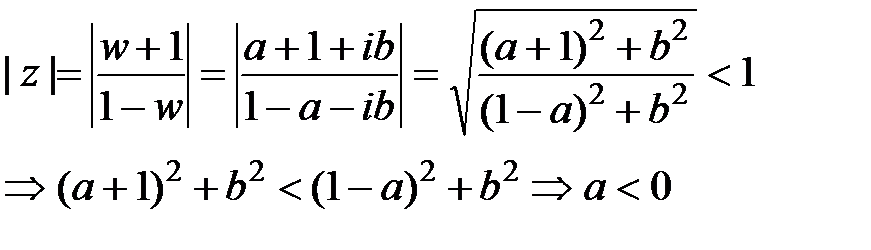
Таким образом, условие | z | < 1 равносильно требованию

Re w < 0.

Положив z = (w +1)/(1– w) и подставив в характеристическое уравнение, получим

a ₀(w +1) ^m + a ₁(w +1) ^{m -1}(1– w) + … + a_{m -1}(w +1)(1– w) ^{m -1} + a_m (1– w) ^m =
A ₀ w^m + A ₁ w^{m -1} + … + A_m = 0,

где

Так как | z | < 1 при Re w < 0, то для проверки условия Re w < 0 можно воспользоваться критерием Гурвица. Например, характеристическое уравнение после подстановки z =(w +1)/(1– w) приводится к виду

Согласно критерию Гурвица условия устойчивости для системы 2-го порядка имеют вид

Пример. Исследование устойчивости движения поворотной платформы с дискретным датчиком угла поворота (рис. 4.12).

Рис. 4.12. К исследованию устойчивости поворотной платформы

Чтобы обеспечить вращение поворотной платформы с высокой точностью, используется система автоматического управления с обратной связью и датчиком угла поворота (ДОС).

Упрощенная математическая модель системы имеет вид:

J 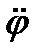= M_д;

M_д = с_мI;

rI = u – c_e .

Если ДОС непрерывный, то управляющее напряжение на двигатель при использовании пропорционально-дифференциального закона управления имеет вид u= K (a Dw + Dj), где Dj = j* – j (j*, j характеризуют желаемую и реальную траектории движения платформы соответственно), Dw = .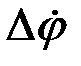

Структурная схема системы приведена на рис. 4.13.

Рис. 4.13. Структурная схема непрерывной системы

Исследуем устойчивость этой системы.

Передаточная функция системы имеет вид

Характеристическое уравнение

где Т _м = Jr / c _e c_м – электромеханическая постоянная времени, k = К / c _e.

По характеристическому уравнению заключаем, что непрерывная система устойчива при любых a, k > 0.

Если ДОС дискретный (или устройство управления имеет дискретный характер), то управляющее напряжение будет изменяться один раз за период следования T сигналов датчика положения:

Du (t)= K (ap +1)Dj(nT), nT £ t < (n +1) T.

Имеем импульсную систему, структурная схема которой приведена на рис. 4.14. Выражение для импульсной передаточной функции системы:

где G _н(p) – передаточная функция непрерывной части системы

Рис. 4.14. Структурная схема импульсной системы

Получим выражение для передаточной функции G _раз(z) разомкнутой системы.

В результате выражение для G _раз(z) принимает вид:

Получим характеристическое уравнение 1 + G _раз(z) = 0:

На основе алгебраического критерия имеем следующие условия устойчивости

При T << T _м может быть получена оценка T < 2 T _м/(1 + a k). Чем больше общий коэффициент усиления разомкнутой цепи, тем меньше должен быть период квантования сигналов обратной связи, т. е. тем чаще должна сниматься информация о текущем состоянии.

Для уравнений высокого порядка исследование устойчивости может выполняться с помощью критерия Найквиста. Для этого используются частотные характеристики импульсных систем.

Поиск по сайту: