Поведение нелинейных систем на фазовой плоскости

Исследование поведения нелинейных систем второго порядка на фазовой плоскости целесообразно начинать с определения положений равновесия – особых точек фазового портрета. Принципиальным отличием нелинейных систем от линейных является то, что положений равновесия может быть несколько или они могут отсутствовать вообще.

Если в окрестности изолированных положений равновесия нелинейности достаточно гладкие, то записывают линеаризованные дифференциальные уравнения для малых отклонений от конкретных положений равновесия. По расположению собственных значений матриц или корней характеристического полинома устанавливаются типы особых точек, как это показано ранее в 5.2.2. В окрестности изолированных особых точек ― положений равновесия ― фазовые портреты нелинейных систем похожи на фазовые портреты соответствующих линеаризованных систем. По мере удаления от точек равновесия фазовые портреты нелинейных систем могут иметь качественные отличия.

Для построения фазовых траекторий используют графические, аналитические и численные методы.

Наиболее простым графическим методом решения дифференциальных уравнений (5.4), (5.8) является метод изоклин. Изоклина ― кривая равного наклона касательных к фазовым траекториям. Ее уравнение получается приравниванием правых частей (5.3) или (5.7) заданному наклону c:

Параметр c семейства изоклин равен тангенсу угла наклона касательных к фазовым траекториям. Совокупность наклонов c_i выбирается так, чтобы изменение угла между двумя соседними изоклинами было примерно одинаковым.

Пример. Решение уравнения 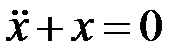графическим методом.

Приводим уравнение к виду:

Строим изоклины для различных начальных условий. В каждой точке изоклины строим короткий отрезок под углом α = arctg c, получая следующую точку. По полученным отрезкам (направлениям) строим интегральные кривые (рис. 5.12).

Рис. 5.12. Изоклины и интегральные кривые

Для построения изоклины берем на фазовой плоскости точку с конкретными начальными условиями, например,
х ₁ =1, х ₂ = 0, вычисляем с = –1/0 = –¥ и строим короткий отрезок под углом α = arctg c = –90°; попадаем в точку (1; –0,1).

В этой точке с = –1/(–0,1) = 10, α = arctg10 = 84°. Строим короткий отрезок под углом α = arctg c = –84°; попадаем в точку (0,95; –0,2).

В этой точке с = –0,95/–0,2 = 4,75, α = arctg4,75 = 78°.

Продолжаем процесс дальше.

Попадаем в точку (0; –1). В этой точке с = –0/(–1) = 0, α = arctg0 = 0°. Строим короткий отрезок под углом α = arctg 0 = 0° и т. д.

После этого соединяем все полученные точки гладкой кривой и получаем частное решение – интегральную кривую. Выбирая различные начальные условия, получим семейство интегральных кривых, которое и дает решение дифференциального уравнения.

В некоторых случаях возможно аналитическое решение дифференциальных уравнений для фазовых траекторий (5.3), (5.7).

Пример. Фазовый портрет математического маятника.

Рассмотрим уравнение математического маятника

Маятник имеет счетное множество положений равновесия: j= np; n = 0, ±1, ±2,....

Линеаризованное уравнение для малых отклонений от нижних положений равновесия (четных n) имеет вид , а для отклонений от верхних положений равновесия (нечетных n): .

Характеристический полином дифференциального уравнения для нижних положений равновесия Q (р) = р ² + k ² = 0 имеет пару мнимых корней р _1,2 = ± i×k. Следовательно, этим положениям равновесия отвечает особая точка типа “центр”. Характеристический полином для верхних положений равновесия Q (р) = р ² – k ² = 0 имеет действительные корни разных знаков р ₁ = + k, р ₂ = – k; этим положениям равновесия отвечает особая точка типа “седло” (рис. 5.12).

Рис. 5.12. Фазовый портрет маятника

Видим, что при изменении параметров системы качественные свойства особой точки (тип особой точки) изменяются. Изменение типа особой точки системы при изменении значений ее параметров называется бифуркацией. Сепаратрисы, образованные слиянием искривленных “усов” седел, оказываются границами областей с колебательным движением; незамкнутые траектории вне этих областей изображают неравномерные вращательные движения маятника вокруг точки подвеса.

Для получения аналитических выражений для фазовых траекторий маятника запишем его дифференциальное уравнение в форме Коши:

Деление второго уравнения на первое дает дифференциальное уравнение первого порядка:

решая которое при различных начальных условиях (j₁₀, j₂₀), получаем выражения для интегральных кривых на плоскости (j₁, j₂).

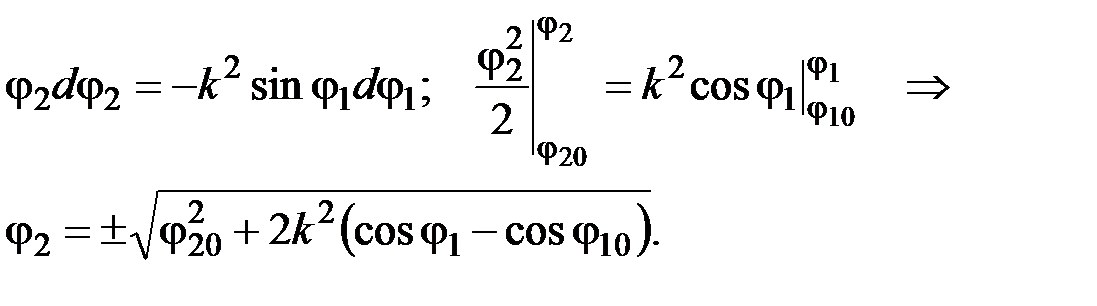
Фазовый портрет маятника изображен на рис. 5.12.

В случае линейных систем автоматического управления характер (тип) особой точки определяет движение системы при любых отклонениях от состояния равновесия. Для нелинейных систем характер особой точки определяет поведение фазовых траекторий лишь в некоторой малой окрестности особой точки. При рассмотрении поведения фазовых траекторий нелинейных систем на всей фазовой плоскости весьма важную роль играют особые траектории.

Поиск по сайту: