 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Частотные критерии устойчивости
На практике алгебраические критерии применяют к системам невысокого порядка (n < 5...6). При более высоком порядке системы применение алгебраических критериев становится неэффективным из-за резко возрастающей трудоемкости вычислений. В этом случае для анализа устойчивости применяют частотные критерии, основным из которых является критерий Найквиста. Критерий Найквиста позволяет не только установить сам факт устойчивости или неустойчивости системы, но и определить запасы устойчивости.
Критерий Михайлова
Пусть Q (l) – характеристический полином системы. По Q (l) строится кривая Михайлова – АФХ характеристического полинома.
l ® i w Þ Q (i w) = a 0(i w) n + a 1(i w) n -1 + … + an -1(i w)1 + an,
Re Q (i w) = an – an -2w2 + an -4w4 – …; Im Q (i w) = an -1w – an -3w3 + an -5w5 – …
Чтобы система была устойчивой, необходимо и достаточно, чтобы кривая Михайлова проходила через «n» квадрантов (или делала поворот на угол Dj = n ×p/2, где n – порядок характеристического полинома (порядок характеристического уравнения).
Замечания.
1. Наибольший возможный угол поворота Dj £ n ×p/2.
2. Всегда Dj = k ×p/2 (k – целое), т. е. кривая Михайлова проходит целое число квадрантов; для устойчивой системы – k = n, для неустойчивой системы – k < n.
3. Dj = p/2×(n – 2 N +), где N + – число «неустойчивых корней» (корней с положительной вещественной частью).
4. Если система устойчива, то j(w) – монотонная функция.
5. Критерий можно применять для исследования устойчивости как замкнутых, так и разомкнутых систем (в последнем случае нужно рассматривать характеристический полином разомкнутой системы).
Другая формулировка критерия Михайлова. Для устойчивости линейной системы при положительных коэффициентах характеристического уравнения, необходимо и достаточно, чтобы кривые X (w) = Re Q (i w) и Y (w) = Im Q (i w) имели в сумме число пересечений с осью абсцисс равное порядку n уравнения и чтобы абсциссы этих точек перемежались.
Пример.
Q (p) = p 3+3 p 2+2 p +1
| ReQ (i w) |
| w |
| X (w), Y (w) |
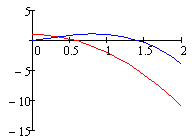
| ImQ (i w) |
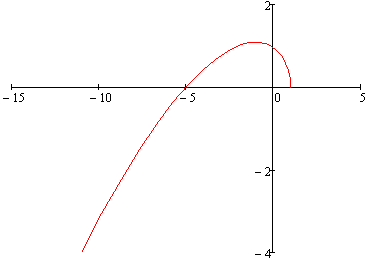
Рис. 2.40. АФХ устойчивой системы
Пример. Q (p) = 3 p 3+ p 2+ p +2.
| X (w), Y (w) |
| ImQ (i w) |
| ReQ (i w) |
| w |
Рис. 2.41. АФХ неустойчивой системы
Критерий Найквиста
Критерий Найквиста позволяет судить об устойчивости САУ по характеристикам ее разомкнутой части. Поэтому для его использования система должна быть приведена к стандартной форме (с единичной отрицательной обратной связью, рис. 2.42).
x (t) y (t) G раз(p) – ПФ разомкнутой системы
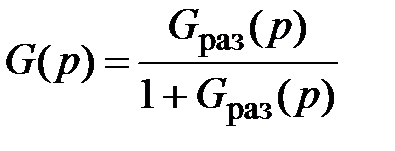 G раз(p)
G раз(p)
Рис. 2.42. Стандартная форма представления системы
Формулировка критерия зависит от устойчивости разомкнутой системы.
1. Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы было равно нулю суммарное число пересечений амплитудно-фазовой характеристикой разомкнутой системы отрезка вещественной оси (–1; –¥). При этом пересечению снизу вверх присваивается значение –1, а пересечению сверху вниз +1 (рис. 2.44).
2. Если разомкнутая система находится на границе устойчивости, то для устойчивости замкнутой системы необходимо и достаточно, чтобы было равно нулю суммарное число пересечений амплитудно-фазовой характеристикой отрезка вещественной оси (–1; –¥), дополненной в точках разрыва дугами бесконечно большого радиуса.
3. Если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы суммарное число пересечений амплитудно-фазовой характеристикой отрезка вещественной оси (-1; -¥) было равно N +/2, где N + – число неустойчивых корней.
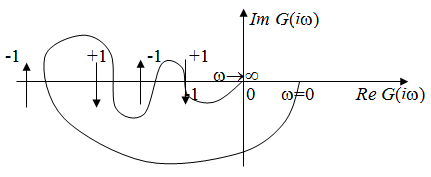
Рис. 2.43. К подсчету числа пересечений
Разомкнутая система находится на границе устойчивости, если ее характеристический полином (знаменатель передаточной функции разомкнутой системы) имеет корни с нулевой вещественной частью. В случае нулевых корней АФЧХ разомкнутой системы имеет разрыв при ω = 0. Этот разрыв равен –π∙ m /2, где m – кратность нулевого корня. Поэтому АФЧХ следует дополнить дугой, равной –π∙ m /2, начинающейся с положительной вещественной полуоси (рис. 2.44, радиус дуги R = µ).
| w=0 |
| R =¥, j=-p/2 |
| Re G (i w) |
| Im G (i w) |
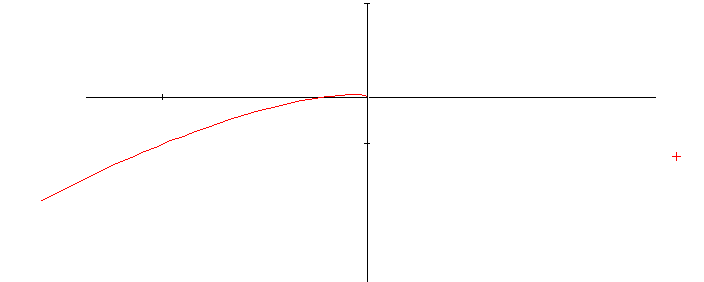
Рис. 2.44. Разрыв АФЧХ при ω = 0
Если же характеристический полином разомкнутой системы имеет чисто мнимые корни, соответствующие звеньям с ПФ 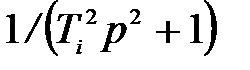 , то разрыв имеет место в точках ω i = 1/ Ti и равен -π. Поэтому АФЧХ в каждой подобной точке дополняется дугой равной -π (рис. 2.45).
, то разрыв имеет место в точках ω i = 1/ Ti и равен -π. Поэтому АФЧХ в каждой подобной точке дополняется дугой равной -π (рис. 2.45).
Наиболее удобно применять критерий Найквиста в терминах логарифмических частотных характеристик.
| w=1/ T |
| w=1/ T |
| R =¥, j=-p |
| Re G (i w) |
| Im G (i w) |

Рис. 2.45. Разрыв АФЧХ при ω = 1/ Т
Критерий Найквиста в терминах логарифмических
частотных характеристик
Для применения критерия Найквиста при исследовании замкнутой системы с единичной отрицательной обратной связью (система должна быть предварительно приведена к указанному виду) строятся логарифмические частотные характеристики разомкнутой системы. Итак, об устойчивости замкнутой системы судят по характеристикам ее разомкнутой части. Вся «прелесть» использования критерия Найквиста заключается в том, что логарифмические частотные характеристики разомкнутой системы обычно легко построить.
Рассматривается область частот, где L (w) > 0. На этом участке считается число пересечений фазовой характеристикой уровней
–p ± 2p k (k – целое число). Фазовая характеристика должна быть дополнена в точках разрыва. Разрывы могут быть двух видов. Разрывы первого вида имеют место при w = 0, если G раз(p) имеет m нулевых полюсов. Фазовая характеристика при w = 0 имеет скачок вниз на - m p/2. Разрывы второго вида имеют место при w = 1/ T, если G раз(p) имеет чисто мнимые полюсы ± i ×1/ T (в знаменателе сомножители вида T 2 p 2+1). Фазовая характеристика при w = 1/ T имеет скачок вниз на -p. Если скачок происходит через уровень -p ± 2p k, то соответствующее пересечение учитывается.
1. Если разомкнутая система устойчива или находится на границе устойчивости, то для устойчивости замкнутой системы необходимо и достаточно, чтобы равнялось нулю суммарное число пересечений ЛФХ уровня –p ± 2p k в области частот, где L (w) > 0. Пересечению ЛФХ уровня -p ± 2p k сверху вниз присваивается -1, снизу вверх - +1. Если фазовая характеристика начинается с этого уровня, такому пересечению присваивается соответственно -1/2 или
+ 1/2.
2. Если разомкнутая система неустойчива (имеет N+ корней с положительной вещественной частью), то для устойчивости замкнутой системы необходимо и достаточно, чтобы суммарное число пересечений ЛФХ уровня –p±2p k в области частот, где L (w) > 0 было равно N+ /2.
Резюме. Для исследования устойчивости линейной САУ по критерию Найквиста следует:
1. Привести систему к стандартному виду (с единичной отрицательной обратной связью).
2. Привести выражение для передаточной функции разомкнутой части системы к стандартной форме (произведению передаточных функций элементарных звеньев).
3. Исследовать устойчивость разомкнутой системы (по корням характеристического полинома – знаменателя передаточной функции).
4. Построить логарифмические частотные характеристики разомкнутой системы.
5. Воспользоваться соответствующей формулировкой критерия Найквиста в терминах логарифмических частотных характеристик.
Поиск по сайту: