Цифровые модели непрерывных систем

Прямое Z -преобразование передаточной функции непрерывной системы, а точнее, Z -преобразование переходной функции непрерывной системы, как правило, приводит к громоздким вычислениям, а при неизвестных полюсах передаточной функции к тому же точных решений не имеет. Существует несколько приближенных методов построения цифровых моделей. В большинстве своем эти методы основаны на разложении аргумента Z -преобразования в ряды. Здесь рассмотрим три приема: метод прямой разности, метод обратной разности и метод билинейного преобразования.

Метод прямой разности. Выделяя в обычном разложении аргумента

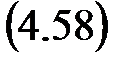
линейное приближение z» 1 + pT, найдем p» (z – 1 ) / T.

Используя эту подстановку, из передаточной функции непрерывной системы G _н(p) получают цифровую модель G (z) = G _н((z – 1 ) / T).

Этот прием получил название метода прямой разности, а в численных методах он известен как метод прямоугольников с упреждением.

Метод обратной разност и. Рассмотрим разложение

Первое приближение его составляет z» 1/(1 – pT). Отсюда следует, что подстановка p» (z – 1 ) / zT приводит к цифровой модели по методу обратной разности, известному также как метод прямоугольников.

Метод билинейного преобразования. Используем представление аргумента z рядом

Выделяя здесь вновь первое приближение, получим

откуда следует очередная z -форма или билинейная подстановка .

Использование билинейной подстановки дает цифровую модель по методу билинейного преобразования, известному также как метод трапеций.

Итак, цифровая модель часто позволяет значительно упростить исследование непрерывной системы и вместо дифференциальных уравнений перейти к разностным. Важным вопросом цифрового моделирования является выбор периода квантования, так как он является определяющим в проблеме эквивалентности непрерывной системы и ее цифровой модели. Условия эквивалентности системы и ее модели зависят от выбора критерия эквивалентности. Так, если критерием эквивалентности принять требование устойчивости исходной системы и ее цифровой модели, то в большинстве случаев можно ограничиться условием Котельникова

Т < p / w₀,

где Т – период квантования, w₀ – собственная частота системы.

Требования к периоду квантования значительно ужесточаются, если критерием эквивалентности служит точность исходной системы и ее цифровой модели. Оценка ошибки е цифрового моделирования по методу прямой и обратной разности имеет вид е < w ТA (0)/2, а по методу билинейного преобразования е < w² Т ² A (0)×(М –1)/12, где w – круговая частота воспроизводимого сигнала, М – колебательность системы, А (0) – начальное значение модуля частотной характеристики.

Приведенные оценки позволяют обоснованно выбрать период квантования цифровых моделей.

5 Исследование нелинейных САУ

Линейные автоматические системы являются, как правило, идеализированными моделями реальных систем, которые всегда не линейны. Нелинейности могут быть обусловлены внутренними свойствами системы (ограниченными энергетическими ресурсами, технологическими характеристиками, погрешностями изготовления элементов), но могут вводиться специально для улучшения динамических свойств системы в целом. Например, нелинейные алгоритмы управления могут обеспечить максимальное быстродействие процессов при наличии естественных ограничений на уровни управляющих воздействий; нелинейности обязательно вводятся при создании генераторов колебаний и т. д. В ряде систем управления техническими объектами нелинейные, в частности, релейные регулирующие устройства оказываются наиболее простыми, дешевыми и надежными.

Нелинейной системой автоматического управления называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением (алгебраическим или дифференциальным).

Нелинейности можно разделить на существенные и несущественные. Пренебрежение существенными нелинейностями ведет к искажению качественных явлений и свойств системы и потому недопустимо. Важная особенность нелинейностей состоит в несправедливости для включающих их систем принципа суперпозиции. Поэтому математический аппарат исследования линейных САУ (преобразования Лапласа и Фурье) оказывается недостаточным для исследования нелинейных систем.

Поиск по сайту: