 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Астатизм
С коэффициентами ошибок связано понятие астатизма. Астатическими называются системы, точно (с нулевой ошибкой) отрабатывающие любые постоянные воздействия. Система называется астатической m -го порядка, если при полиномиальных воздействиях x (t) = a 0 + a 1 t +...+ am -1 tm -1, n (t) = b 0+...+ bm -1 tm -1 вынужденный процесс изменения ошибки отсутствует (т. е. установившаяся ошибка e уст(t) равна нулю).
Для астатической системы 1-го порядка с 0 = 0, с 1 ¹ 0, для астатической системы 2-го порядка с 0 = 0, с 1= 0, с 2 ¹ 0, для астатической системы m -го порядка с 0 = 0,..., сm -1 = 0, сm ¹ 0.
Отметим некоторые свойства астатических систем
· Для системы с астатизмом (1-го порядка) установившаяся ошибка не зависит от самого сигнала (так как с 0 = 0). Если x (t) = x 0, то e (t) = 0, так как x ( i )(t) = 0.
· Если подан линейный сигнал x (t) = a 0 + a 1 t, то для астатической системы e уст(t) = a 1 с 1, т. е. ошибка постоянна и определяется скоростью изменения входного сигнала. Если подан квадратичный сигнал x (t) = a 0 + a 1 t + a 2 t 2, то e уст(t) = (a 1 + a 2 t) с 1 + a 2 с 2, т. е. e уст(t)» a 2 с 1 t ® ¥ и при t ®¥, система с астатизмом 1-го порядка не «успевает» следовать за сигналом; ошибка нарастает со временем.
· Свойства астатизма определяются наличием интеграторов. Количество интеграторов определяет порядок астатизма.
Пример. Астатизм 1-го порядка.
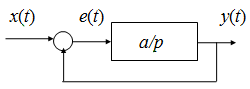
Gy/x (p) = a /(a+p); Ge/x (p) = p /(a+p); c 0 = Ge/x (0) = 0; c 1= G (1) e/x (0) = [ p /(a+p)]0 =1/ a.
Итак,для системы с астатизмом 1-го порядка коэффициент ошибки по положению равен нулю, а коэффициент ошибки по скорости – величина обратная общему коэффициенту усиления разомкнутой системы:
c 0 = 0; c 1 = 1/ a.
e (t) = Ge/x (p) x (t) = p/ (a+p) x (t) Þ (a+p) e(t) = px (t) Þ
ae (1)(t) + e (t) = x (1)(t) Þ
ошибка не зависит от самого сигнала, а только от скорости его изменения.
При постоянном входном сигнале x (t) = x 0 Þ e уст(t) = 0.
При линейном входном сигнале x (t) = a 0 + a 1 t Þ e уст(t) = a 1/ a = Const.
Ничего качественно не изменится, если G (p) имеет более сложный вид, например
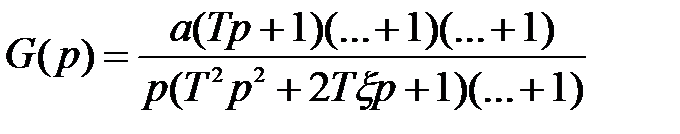
Легко проверить, что и в этом случае получим c 0 = 0; c 1 = 1/ a.
Пример.

c 0 = 0; c 1 = 0; c 2 ¹ 0; x (t) =1[ t ] Þ e (t) = 0;
x (t) = a0 +a1 t Þ e (t) = 0;
x (t) = a0 +a1 t +a2 t 2 Þ e (t) = 2 c 2a2 ¹ 0 – появляется ошибка отслеживания.
Увеличение числа интеграторов приводит к росту точности.
Относительно астатизма по помехам справедливы те же выводы (рассматривать нужно соответствующие передаточные функции).
Пример. Найти коэффициенты ошибок по положению и скорости для полезного сигнала x (t) и возмущения n (t) для следующей системы (k = 8).

Рис. 2.50. Структурная схема
Для коэффициентов ошибок по полезному сигналу имеем:
c 0 = 0, c 1 = 1/(0,4×8)» 0,3. Для вычисления коэффициентов ошибок по возмущению определим передаточную функцию Ge/n (p):
 .
.
d 0 = 20/32 = 5/8;
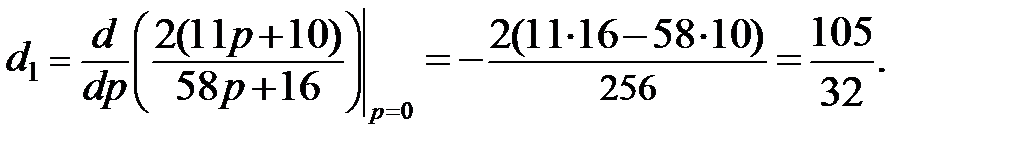
Поиск по сайту: