Методические указания. При выполнении работы необходимо учесть следующие замечания

При выполнении работы необходимо учесть следующие замечания.

1. Во введении при доказательстве статизма или астатизма системы можно воспользоваться следующим рассуждением, например, для схемы А по отношению к входному сигналу при отсутствии нагрузки:

Предположим, что система является астатической, т.е. в установившемся режиме рассогласование равно нулю. Тогда на выходе усилителя напряжение отсутствует и на двигатель напряжение не поступает, и ротор неподвижен. В этом случае рассогласование между входным сигналом и нулевым напряжением на выходе тахогенератора равно , т.е. не равно нулю, что противоречит исходному предположению. Тем самым рассогласование в установившемся режиме не равно нулю и система является статической по отношению к входному сигналу .

При доказательстве статизма системы по отношению к возмущению рассматривается изменение установившейся ошибки при наличии входного сигнала . В качестве критерия противоречия может использоваться закон сохранения энергии и др.

2. Математическое описание каждого функционального элемента следует проводить в отдельном подразделе с указанием заголовка, например:

1.1. Генератор постоянного тока

1.2. Двигатель постоянного тока

и т.д.

Для каждого функционального элемента привести его принципиальную схему, дать краткое описание принципа действия (например, пояснить каким образом достигается усиление сигнала по мощности в генераторе и ЭМУ).

При выводе уравнений функциональных элементов с учетом принятых допущений нет необходимости проводить линеаризацию уравнений и записывать уравнения в малых отклонениях от номинального режима. Здесь уравнения функциональных элементов линейные и изменение их координат могут быть большими.

При записи уравнений и передаточных функций рекомендуется использовать следующий способ обозначений: например, – коэффициент усиления электронного усилителя, – передаточная функция электронного усилителя; , где – передаточная функция, связывающая выход с входом и т.п. (другие обозначения см. ниже).

Допускается сквозная нумерация формул или нумерация формул в пределах одного раздела (например, (2.4) и т.п.).

3. Определение параметров электрических машин проводится по паспортным данным таблицы 1, которые соответствуют номинальным режимам при источнике питания бесконечной мощности (с нулевым внутренним сопротивлением). При этом коэффициенты передачи определяются из уравнений статики. С помощью найденных паспортных значений коэффициентов передачи определяются коэффициенты передачи и постоянные времени для соединенных блоков функциональных элементов ("электронный усилитель-ЭМУ" в схемах А, Б, В; "электронный усилитель-генератор" в схемах Г, Д; "генератор-двигатель" в схемах А, Б, Г, Д) с учетом внутренних сопротивлений источников напряжения.

Расчеты проводятся в системе единиц СИ.

Например:

1.1.1. Определение параметров генератор постоянного тока

1) Уравнения статики для номинального режима генератора имеют вид

,

,

,

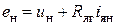где и – номинальные напряжение и ток в обмотке возбуждения генератора, – номинальное значение э.д.с.

Отсюда следует, что

,

и с учетом паспортных значений найдем коэффициент усиления генератора

.

Например, для генератора №1 получим

.

2) Уравнения динамики генератора в схеме соединения имеют вид

,

,

где , , – сопротивление якоря ЭМУ – для схем А, Б, В; , , – выходное сопротивление электронного усилителя – для схем Г, Д.

Отсюда с учетом преобразования Лапласа при нулевых начальных условиях получим с передаточной функцией

,

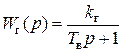где , .

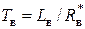Например, коэффициент усиления генератора для схем Г, Д имеет значение

,

т.е. меньше паспортного значения.

3) Для генератора с нагрузкой в схеме В напряжение на нагрузке определяется по формуле

,

где ; 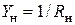– проводимость нагрузки. Отсюда следует, что напряжение является нелинейной функцией от величин , . Учитывая, что при наличии нагрузки Ом величина 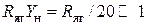, с помощью разложения в ряд Тейлора можно записать

.

В установившемся номинальном режиме при отсутствии нагрузки () справедливо уравнение

.

Учитывая малость величины 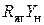, отклонения , вызванные подключением нагрузки , также будут малыми. Тогда при отбрасывании слагаемого второго порядка малости будет справедливо уравнение

.

1.2.1. Определение параметров двигателя постоянного тока

1) Уравнения статики для номинального режима имеют вид

,

,

где – коэффициент противо - ЭДС якоря, 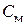– коэффициент вращающего момента. При единице измерения рад/с в системе единиц СИ выполняется равенство с размерностью [8, с.25]. Тем самым найдем

, .

Например, для двигателя №1 получим

, .

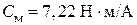2) Уравнения динамики двигателя в схеме соединения имеют вид

,

,

где , ; при этом – для схем А, Б; – момент нагрузки приведенный к валу двигателя для схем Г, Д.

Отсюда с учетом преобразования Лапласа при нулевых начальных условиях найдем:

,

где , , , , .

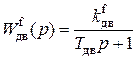Для схем Г, Д выходной координатой двигателя является угол поворота ротора , т.е. и, следовательно,

,

где , .

Например, для двигателя и генератора №1 получим

,

с.

1.3.1. Определение параметров ЭМУ

1) С учетом принятых допущений о полной компенсации реакции якоря в цепи нагрузки ЭМУ, уравнения статики для номинального режима имеют вид

,

,

,

,

,

где и – номинальные напряжение и ток в обмотке возбуждения; и – номинальные э.д.с. и ток в короткозамкнутой цепи; , , и – номинальные э.д.с., напряжение, ток и сопротивление якорной цепи нагрузки ЭМУ соответственно; – постоянная угловая скорость вращения якоря вспомогательного двигателя.

Исключая переменные и получим

.

Отсюда найдем

.

Например, для ЭМУ №1 получим

.

2) Уравнения динамики ЭМУ в схеме соединения имеют вид

,

– для схем А, В;

– для схемы Б (объяснить почему),

,

,

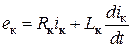где , – ток во вторичной обмотке трансформатора схемы Б.

Отсюда с учетом преобразования Лапласа при нулевых начальных условиях найдем:

1) для схем А, В:

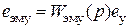
с передаточной функцией

,

где , , .

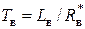2) в схемах Б, В предусмотрена гибкая дифференцирующая обратная связь, предназначенная для гашения возможных колебательных процессов в электромашинной системе при больших коэффициентах усиления ЭМУ. Сигнал отрицательной обратной связи снимается с зажимов выхода ЭМУ в соответствии со схемой рис.8, где – операционное сопротивление обмотки возбуждения генератора. При этом

,

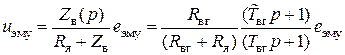где , . Учитывая, что , можно принять

.

Например, для генератора и ЭМУ №1 получим

.

а) В схеме Б обратная связь осуществляется с помощью стабилизирующего трансформатора, уравнения которого имеют вид [8, стр.68; 9, стр. 17]

,

,

где и – ток в первичной и вторичной обмотке соответственно; – взаимная индукция обмоток; – общее сопротивление вторичной обмотки. Исключая из уравнений ток , получим выражение для тока :

,

где , , , 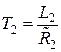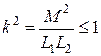. Поскольку в трансформаторе со стальным сердечником коэффициент , то получим уравнение

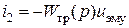
с упрощенной передаточной функцией трансформатора, содержащего дифференцирующее звено:

,

где .

Тогда с учетом обратной связи по току , в соответствии со структурной схемой рис. 9 найдем зависимость , где эквивалентная передаточная функция имеет вид

,

где .

Рис. 9

Раскладывая выражение в квадратных скобках знаменателя, окончательно получим

,

где , .

б) В схеме Б обратная связь осуществляется с помощью форсирующей - цепи с передаточной функцией согласно структурной схеме рис. 10.

Рис. 10

Передаточная функция форсирующей - цепи имеет вид

,

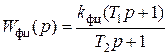где , , . Поскольку 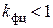, то выполняется неравенство .

По заданным численным значениям найдем

, с, с.

Поскольку постоянная времени значительно меньше постоянной времени и постоянных времени других функциональных элементов схемы, можно принять 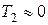. При этом упрощенная передаточная функция форсирующей - цепи имеет вид

,

т.е. содержит производную от входного сигнала.

Тогда в соответствии со структурной схемой рис. 10 найдем зависимость с эквивалентной передаточной функцией

,

где ; , , .

4. При определении передаточных функций замкнутых систем следует использовать передаточные функции разомкнутых систем. Для этого можно использовать следующее правило для структурных схем с одним контуром обратной связи:

в числителе передаточной функции указывается произведение передаточных функций с учетом знаков, через которые проходит входной сигнал до заданного выходного сигнала кротчайшим путем; в знаменателе передаточной функции указывается выражение , где – передаточная функция разомкнутой системы, равная произведению передаточных функций от сигнала рассогласования до сигнала главной отрицательной обратной связи, поступающего на устройство сравнения.

В качестве примера рассмотрим структурную схему системы для схемы Д, представленную на рис. 11. Данная схема содержит два контура: контур местной отрицательной обратной связи по сигналу и контур главной отрицательной обратной связи по сигналу . Приведенное правило используется для каждого контура.

Найдем, например, зависимость , т.е. определим передаточные функции , .

а) Выпишем выражение для передаточной функции , для этого установим путь сигнала до сигнала 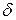, которыый проходит через устройство сравнения с коэффициентом передачи равным единице. Следовательно, числителем передаточной функции является единица. При определении передаточной функции разомкнутой системы сигнал проходит через контур с местной обратной связью, для которого в свою очередь зависимость выхода от входа через передаточную функцию согласно правилу определяется по формуле

.

Здесь в числителе указывается произведение передаточных функций кратчайшего пути от входа к выходу , в знаменателе выражение с передаточной функцией разомкнутой системы внутреннего контура .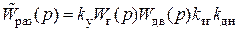

Тогда передаточная функция определяется по формуле

,

а искомая передаточная функция имеет вид

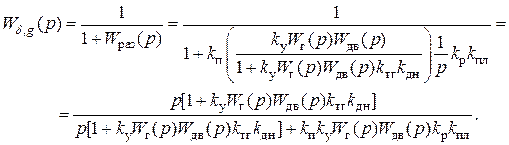
б) Аналогично определяется передаточная функция . Сначала опре­деляется связь выхода со входом для внутреннего контура с помощью передаточной функции

,

где знак "–" соответствует знаку сигнала на устройстве сравнения. Затем при движе­нии по контуру от сигнала до сигнала 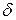окончательно находим вид передаточной функции

5. Для определения коэффициента усиления электронного усилителя по заданным условиям точности в установившемся режиме необходимо использовать формулу о конечном значении оригинала. Например, для схемы Д с учетом предыдущего получим

,

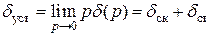где – скоростная ошибка при (), – статическая ошибка при ().

С учетом выражений для передаточных функций получим

По заданным условиям точности в установившемся режиме найдем:

Данную формулу удобно использовать для определения

9. При построении ЛФХ воспользоваться шаблонами, вырезанными

из ватмана.

Масштаб построения ЛФХ и ЛАХ: I град - I мм и 20 дБ - 40 мм;

масштаб по оси частот - одна декада - 100 мм; Д-кривые и годограф Михайлова можно чертить без соблюдения масштабов.

10. При изображении графиков указать наименование, размерность, масштабы величин, откладываемых по осям координат.

Д-разбиения по общему коэффициенту усиления. Сделать разметку Д-областей, построив с этой целью годограф Михайлова для одной из точек Д-областей. Определить критический коэффициент усиления и сравнить с коэффициентом усиления, найденным в.п.6 [2, с.148; 4, с.153]. Расчеты провести на ЭВМ.

Характеристики данных нелинейных элементов принадлежат сектору

,

т.е. для систем стабилизации (схемы А, Б, В) замкнутая система может быть исследована на абсолютную устойчивость.

, учитывая, что главная обратная связь системы имеет коэффициент передачи отличный от единицы.

Литература

Основная литература

1. Айзерман М.А. Теория автоматического регулирования. М., Наука, 1966.

2. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М., Наука, 1972.

3. Васильев Д. В., Чуич В.Г., Системы автоматического управления. М., Высшая школа, 1967.

4. Воронов А. А. Основы теории автоматического регулирования. ч.1,2. М.-Л., Энергия, 1965.

5. Техническая кибернетика. Теория автоматического управления. Под. ред. В.В. Солодовникова. Кн.1. М., Машиностроение, 1967.

6. Дегтярев Г.Л. и др. Методы динамического расчета САУ. Казань: КАИ, 1986.

7. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования. М., Машиностроение, 1985.

8. Сабинин Ю.А. Электромашинные устройства автоматики. Л.: Энергоатомиздат. Ленинг. отд-ние, 1988.

9. Сборник задач по теории автоматического регулирования /Под ред Бессекерского В.А.

10. Гаркушенко В.И., Земляков А.С., Файзутдинов Р.Н. Нелинейные и дискретные системы автоматического управления. Уч. пособие. Казань: КГТУ им. А.Н.Туполева, 2000.

Дополнительная литература

6. Воронов А.А. и др. Теория автоматического управления. Ч.1. М., высшая школа, 1977.

7. Основы автоматического управления. Под. ред. В.С. Пугачева. М., Наука, 1978.

8. Цыпкин Я.3. Основы теории автоматических систем. М., Наука, 1977.

9. Техническая кибернетика. Теория автоматического управления. Под. ред. В.В. Солодовникова. Кн. 2. М., Машиностроение, 1967.

10. Бесекерский В.А. и др. Сборник задач по теории автоматического регулирования. М., Наука. 1965.

11. Методы классической и современной теории автоматического управления. Под ред. Егупова Н.Д. М.: МГТУ им.Н.Э.Баумана, 2002. Т.1.

Поиск по сайту: