 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Визначення запасу стійкості замкнутих систем за модулем та фазою.Побудова діаграм Боде
Мета роботи: Ознайомитися з середовищем Matlab, оволодіти методом і сучасним інструментарієм побудови діаграм Боде.
Короткі теоретичні відомості:
Логарифмічний критерій – це частотний критерій, який дозволяє судити про стійкість замкнутої САУ за виглядом логарифмічної характеристики розімкненої системи. Цей критерій грунтується на однозначному зв'язку ЛФЧХ і АФЧХ систем автоматичного управління. При цьому розглядаються САУ, які базуються на використанні стійких розімкнених систем з астатизмом не вище другого порядку.
Як випливає з критерію стійкості Найквіста в стійких САУ фазовий зсув більший ніж (-π) може досягати значення тільки при модулях комплексної передатної функції, меншому ніж одиниця. Це дозволяє легко визначити стійкість за виглядом ЛАЧХ і ЛФЧХ.
Формулювання критерію: ЛДС стійка в розімкненому стані, буде стійкою і в замкненому стані, якщо в діапазоні частот, де L(ω) > 0, значення фази φ(ω) > -π.

Рис. 5.1. ЛФЧХ стійкою і нестійкою САУ
Критичним значенням коефіцієнта перетворення називається таке його значення, при якому АФЧХ проходить через точку (-1, j0) і система знаходиться на межі стійкості.
Запасом по модулю називається величина в дециБеллах, на яку потрібно змінити коефіцієнт перетворення САУ, щоб привести її до межі стійкості.
∆α(ω) = 20 lg |W(ω)|,
де ω 1 — частота, при якій фазова характеристика рівна π.
Запасом стійкості по фазі називається кут, на який потрібно повернути амплитудно-фазову характеристику розімкненої системи, щоб замкнута САУ опинилася на межі стійкості.
∆φ(ωзр) = -π - | φ(ωзр)|,
де φ(ωзр)– значення ФЧХ на частоті зрізу системи, для якої виконується умова 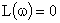 .
.
Хід роботи:
1.Ознайомитися з теоретичними відомостями по темі лабораторної роботи.
2.Далі набрати послідовність команд вказану в прикладі до кожного завдання, натиснути Enter і проаналізувати результат.
3. Оформити звіт.
Завдання №1:
Приклад:
>>num=[0 0 0 5];
>>den=[1 3 3 1];
>>margin(num,den) 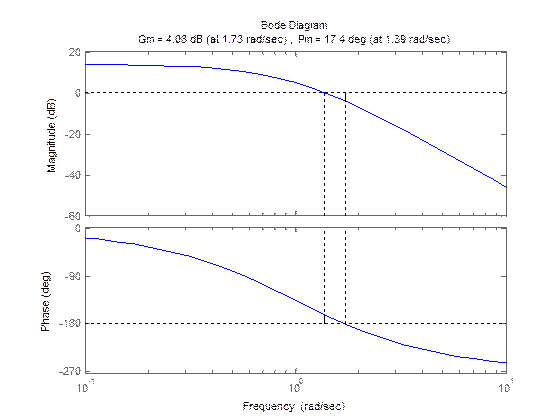
Рис.5.2 Bode Diagram за завданням прикладу №1
| №варіанту | |||||||
| num | |||||||
| den | 0 1 2 3 1 | 0 1 5 5 1 | 0 1 2 3 9 | 0 1 7 3 1 | 0 1 3 1 1 | 0 1 4 6 1 | 0 1 6 4 8 |
| 0 1 2 4 1 | 0 1 2 7 1 | 0 1 3 5 1 | 0 1 1 5 1 | 0 1 2 6 1 | 0 1 7 1 4 | 0 1 9 3 1 | 0 1 4 3 1 |
Завдання №2:
Приклад:
>>num=[1 14];
>>den=[1 2 5 4 1];
>>margin(num,den)
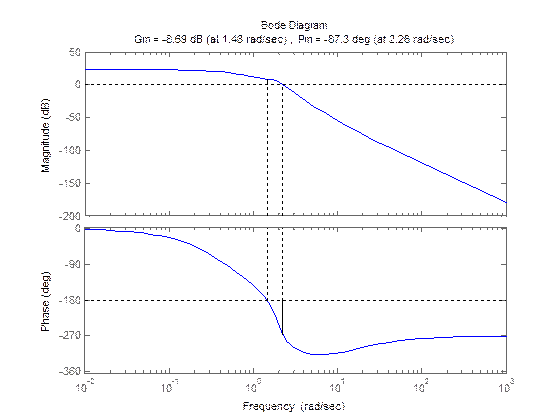
Рис.5.3 Bode Diagram за завданням прикладу №2
| №варіанту | |||||||
| num | 1 2 | 2 25 | 1 15 | 2 10 | 1,5 20 | 1 20 | 3 11 |
| den | 1 2 7 3 1 | 1 2 5 5 1 | 1 2 2 3 1 | 1 8 5 5 1 | 1 2 4 6 1 | 1 1 3 1 1 | 1 1 2 3 1 |
| 2 5 | 3 18 | 3 9 | 3 25 | 2 15 | 4,5 19 | 4 21 | |
| 1 0 3 4 2 | 1 2 3 5 1 | 1 9 8 1 1 | 1 5 3 5 1 | 1 2 7 1 1 | 1 3 2 9 1 | 1 1 2 2 1 | 1 6 2 8 1 |
Рекомендована література:
1. Мирошник И. В. Теория автоматического управления. Линейные системы. Учебное пособие.1-е изд.- Спб.: Питер, 2005.- 336 с.
2. Гальперин М. В. Автоматическое управление. М.: «Форум: ИФРА-м», 2004, 224с.
3. Нитушило А. В. Теория автоматического управления. – М., 1999.
4. Ротач В. В. Теорія автоматичного управління. – М., 1995.
Поиск по сайту: