Моделювання лінійних динамічних систем в середовищі simulink

Мета роботи: Набути практичних навиків, необхідних при дослідженні динамічних процесів, а також закріплення теоретичних знань про перехідні процеси в ланках систем керування.

Короткі теоретичні відомості:

Система Simulink є складовою частиною системи Matlab і призначена для структурно-графічного моделювання різних динамічних об'єктів, як безперервних, так і дискретних. Об’єкт моделювання представляється у вигляді сукупності готових, закінчених блоків, між якими встановлюються зв'язки по типу "вхід-вихід ". При побудові моделі, такі зв'язки зображуються простими стрілками. Можливості (потужність) моделювання динамічного об'єкта визначаються обсягом бібліотек Simulink.

Спосіб конструювання моделі, таким чином, зводиться до вибору відповідних блоків зі складу можливих у бібліотеці: джерел різних сигналів, блоки ланок систем автоматичного управління, логічні блоки або блоки відображення одержуваної інформації. Це надзвичайно спрощує процес моделювання і робить його більш ефективним.

Завданням лабораторної роботи є моделювання і дослідження неперервних аперіодичних та коливних ланок, а також дискретних аперіодичних і дискретних коливних ланок.

Аперіодичною називають ланку, в котрій при подачі на вхід ступінчатого сигналу вихідна величина асимптотично (по експоненті) прямує до нового встановленого значення:

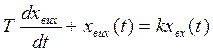, (1)

Де Т – константа часу ланки, характеризує інерційність ланки, с; k – коефіцієнт передачі ланки.

В операторній формі:

(Τp + 1)x_вих(p)= kx_вх(p). (2)

Передатна функція аперіодичної ланки:

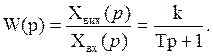(3)

Модель для дослідження динамічних властивостей ланки складається з наступних блоків: Step, Transfer Fcn, Scope.

Для зміни параметрів аперіодичної ланки необхідно двічі клацнути на ній кнопкою миші, з'явиться вікно параметрів ланки Transfer Fcn (рис.2.2).

Параметри ланки Transfer Fcn: Denominator – знаменник передатної функції і Numerator – чисельник у вигляді поліномів с₀pⁿ + с₁p^n-1 +... + с_n і b₀p^m + b₁p^m-1 +... + b_m відповідно. У загальному випадку за допомогою цієї ланки можна задати будь-яку передатну функцію, представлену у вигляді відношення поліномів, причому n ≥ m, де n – порядок полінома в знаменнику, m – порядок полінома в чисельнику.

Рис.2.1 Модель аперіодичної ланки (k=1; T=1)

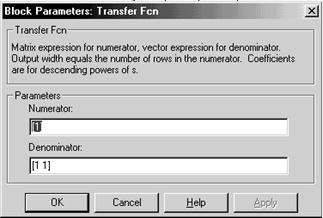
Рис.2.2 Вікно параметрів ланки Transfer Fcn

Рис.2.3. Перехідні та частотні характеристики аперіодичної
ланки (k = 1, T = 1)

Аперіодична ланка другого порядку має вигляд:

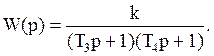(4)

У аперіодичній ланці в чисельнику знаходиться один параметр – коефіцієнт підсилення k, тому у вікні Numerator для аперіодичної ланки вводимо [k]. Знаменник аперіодичної ланки Tp + 1, тобто поліном виду a₀p+ + a₁,де a₀ = T, а₁ = 1. Тому у вікні Denominator для аперіодичної ланки вводимо [a₀ a₁] (через пробіл).

Перехідні та частотні характеристики аперіодичної ланки приведені на рис.2.3.

Коливною називають ланку, у якої при ступінчатій зміні вхідної величини, вихідна величина прагне до нового значенням, здійснюючи при цьому коливання.

Рівняння коливної ланки в операторної формі запису:

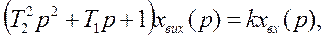(5)

Де T₁ і T₂ – постійні часу коливної ланки; k – коефіцієнт підсилення коливної ланки.

Передатна функція коливної ланки:

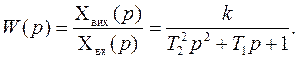(6)

Якщо прийняти

x = Т₁ / 2Т₂. (7)

А також T = T₂,

то передатну функцію можна подати у вигляді:

(8)

Коефіцієнт x називають коефіцієнтом затухання і, судячи з назви, він характеризує затухання перехідного процесу коливної ланки.

Якщо x <1, то перехідний процес ланки - коливний, і чим x менші одиниці, тим більш коливальні процеси.

Якщо x ³ 1, то отримуємо аперіодичну ланку другого порядку.

Модель для дослідження динамічних властивостей ланки складається з наступних блоків: Step, Transfer Fcn, Scope.

Отримана модель показана на рис.2.4.

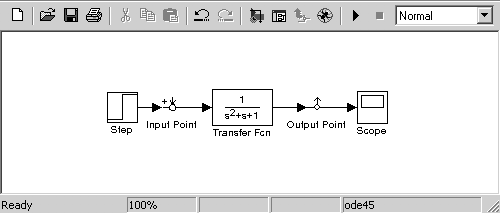
Рис.2.4. Модель коливної ланки (k = 1, T₂² = 1.2 с², T₁ = 1 с)

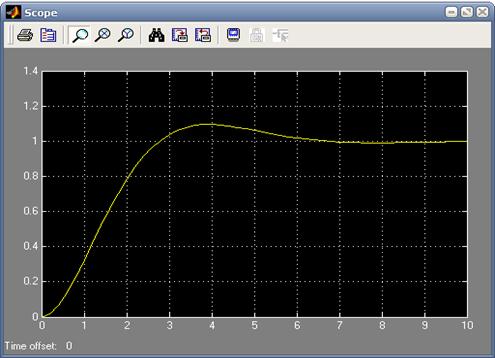
Рис.2.5. Перехідна характеристика коливної
ланки (k = 1, T₂² = 1.2 с², T₁ = 1 с)

Методика зміни коефіцієнтів ланки Transfer Fcn наведено вище для аперіодичної ланки, єдина відмінність – для коливної ланки у вікні Denominator вводимо не два, а три параметри [T₂² T₁ 1] (також через пробіл), оскільки в знаменнику коливальної ланки знаходиться поліном вигляду:

с₀p² + с₁p ¹ + с₂p ⁰, де с₀ = T₂², с₁ = T₁, с₂ = 1.

Перехідні та частотні характеристики коливної ланки представлені на рис.2.5.

Поиск по сайту: