Побудова годографа Михайлова в середовищі matlab

Мета роботи: набути практичних навиків, необхідних при дослідженні динамічних процесів, а також закріпити теоретичні знання про частотні критерії стійкості.

Короткі теоретичні відомості:

Частотні критерії базуються на властивостях частотних характеристик стійких систем. Велику роль в розвитку теорії стійкості відіграв частотний критерій стійкості, запропонований в 1936 році, Михайловим. Так як і алгебраїчні критерії, частотні критерії випливають з безумовної умови наявності тільки «лівих» коренів в характеристичному рівнянні стійкої лінійної динамічної системи. Розглянемо його практичне застосування для аналізу стійкості. Для цього запишемо характеристичне рівняння у виді:

a₀pⁿ+a₁p^n-1+… + a_n-1p+a_n=D(p)

Замінивши в рівнянні p=jω і відділивши дійсну частину від уявної, поліном D(p) приведемо до виду:

D(jω)=a(ω) + b(jω),

Де a(ω) – дійсна частина – сума всіх членів, які включають j в парних степенях; b – уявна частина виразу.

У відповідності з критерієм Михайлова умова стійкості:

Δarg D(jω) = n , 0<ω<∞

Геометричне місце точок кінця вектора D(jω) при зміні частоти в діапазоні 0<ω<∞ називається годографом вектора, або годографом Михайлова. Критерій Михайлова формулюється наступним чином: динамічна система, що описується лінійним диференціальним рівнянням n-го порядку, стійка якщо при зміні ω від 0 до ∞ годограф вектора D(jω) послідовно проходить в додатному напрямку (проти годинникової стрілки) n квадрантів комплексної площини і не перетворюється в 0. На рис.4.1 приведені приклади годографів стійких і нестійких систем.

Рис.4.1 Годографи систем: а – стійких, б- нестійких

Розглянемо приклад побудови годографа в середовищі Matlab.

MATLAB — це назва продукту для числового аналізу та також мова програмування. Це досить простий засіб для роботи з математичними матрицями, малювання функцій, роботи з алгоритмами, створення робочих оболонок (user interfaces) з програмами в інших мовах програмування.

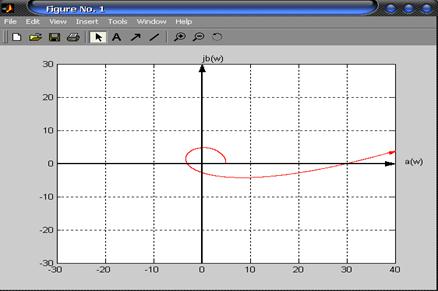
Для побудови годографа Михайлова створимо відповідну програму в середовищі Matlab:

k = 5;
a0 = 10;
a1 = 10;
a2 = 7;
a3 = 3;

a4 = 1;

for w=0.01:0.001:5,
Myh= a4*((w*i)^5) + a3*((w*i)^4) + a2*((w*i)^3) + a1 * ((w*i)^2) + a0*(w*i) + k;
Re = real(Myh);
Im = imag(Myh);
plot(Re, Im)
hold on
end

hold off
grid on
axis([-30 40 -30 30])

Поиск по сайту: