Лабораторна робота № 6

Побудова фазового портрету ЛДС

Мета роботи: Навчитись будувати фазовий портрет лінійної динамічної системи.

Короткі теоретичні відомості:

Моделі, засновані на задачах Коші для ОДР, часто називають динамічними системами, підкреслюючи, що, як правило, вони містять похідні за часом t і описують динаміку деяких параметрів. Проблеми, пов'язані з динамічними системами, насправді різноманітні і часто не зводяться до простого інтегрування ОДР.

Рішення ОДР часто зручніше зображати не у вигляді графіка x_вх (t) x_вих (t),, а у фазовому просторі, по кожній з осей якого відкладаються значення кожній із знайдених функцій. При такій побудові графіку аргумент t присутній на ньому лише параметрично. У даному випадку два ОДР (ми звели до них в попередньому розділі диференціальне рівняння осцилятора другого порядку) фазовий простір є координатною площиною, а рішення є кривою, або, по-іншому, траєкторією, що виходить з точки, координати якої дорівнюють початковим умовам (рис. 6.1). У загальному випадку, якщо система складається з n ОДР, то фазовий простір є n- мірним. При n>3 наочність втрачається, і для візуалізації фазового простору необхідно будувати його різні проекції або вдаватися до інших спеціальних прийомів (наприклад, відображенна Пуанкаре).

Рис. 6.1. Вирішення рівняння w²у' '+vу'+у=0 на фазовій площині

Як правило, вирішення задач Коші для ОДР і їх систем — завдання добре розроблене і з обчислювальної точки зору досить просте. На практиці частіше зустрічаються інші, складніші завдання, зокрема, дослідження поведінки динамічної системи залежно від початкових умов. При цьому в більшості випадків буває необхідним вивчити тільки асимптотичне рішення ОДР. Достатньо наочно можна візуалізувати таку інформацію на фазовій площині, багато в чому завдяки тому, що існує всього декілька типів аттракторів, і для них можна побудувати чітку класифікацію.
З одного боку, кожне розв’язок виходитиме з точки, координати якої є початковими умовами, але, для більшості ОДР цілі сімейства траєкторій закінчуватимуться в одних і тих же аттракторах (стаціонарних точках або граничних циклах). Безліч розв’язків, обчислених для різних початкових умов, утворює фазовий портрет динамічної системи. З обчислювальної точки зору завдання дослідження фазового портрета часто зводиться до звичайного сканування сімейств рішень ОДР при різних початкових умовах.

Для даного прикладу моделі гармонійного осцилятора є єдина стаціонарна точка (аттрактор), на яку "накручується" рішення, з яких би початкових умов воно не виходило. У теорії динамічних систем аттрактор такого типу називається фокусом.

Подальше ускладнення завдань аналізу фазових портретів пов'язане з їх залежністю від параметрів, що входять в систему ОДР. Зокрема, при плавній зміні параметрів моделі може мінятися розташування аттракторов на фазовій площині, а також можуть виникати нові аттрактори і припиняти своє існування старі. У першому випадку, за відсутності особливостей, відбуватиметься просте переміщення ат трактору на фазовій площині (без зміни їх типів і кількості), а в другому — фазовий портрет динамічної системи повністю перебудовується. Критичне поєднання параметрів, при яких фазовий портрет системи якісно змінюється, називається в теорії динамічних систем точкою біфуркації.
Пояснимо поняття біфуркації на прикладі тієї ж моделі осцилятора, яка залежить від двох параметрів (w і v). При р>о існує єдина стаціонарна точка типу фокусу (див. рис. 6.1), яка в точці біфуркації Р=0 вироджується в аттрактор типу центр, що характеризується тим, що рішення ОДР є цикли, що здійснюються навколо цієї точки з амплітудою, яка істотно залежить від початкових умов. Для надійного дослідження фазового портрета практично завжди необхідно вирішити систему ОДР великою кількість разів з різними початковими умовами (і, можливо, з різним набором параметрів моделі), щоб подивитися, до яких аттракторів сходяться різні траєкторії.

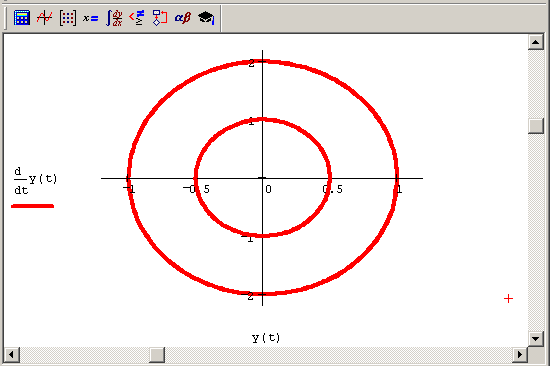
Рис.6.2

Рис. 6.3 Імітаційна модель для побудови фазового портрету

Рис. 6.4 Фазовий портрет лінійної динамічної системи III-го порядку

Поиск по сайту: