Лабораторна робота № 8

Синтез системи керування методом ЛКГ регулятора

Мета роботи: Набути практичних навиків, необхідних при дослідженні синтезу системи керування методом ЛКГ(Лінійний квадратичний Гауссівський) регулятора, а також закріплення теоретичних знань про роботу з відповідним інструментарієм комп’ютерного моделювання.

Короткі теоретичні відомості:

Лінійно-квадратичний гауссівський регулятор - набір методів і математичного апарату теорії управління для синтезу систем управління з від’ємним зворотним зв'язком для лінійних систем з адитивним гауссовских шумом.Синтез проводиться шляхом мінімізації заданого квадратичного функціоналу.

Лінійно-квадратичний гауссівский (ЛКГ) регулятор відноситься до сучасних методів управління. Методологія синтезу контролера дозволяє віднести системи управління, побудовані на такому принципі, до оптимальних систем, в яких оптимізація проводиться за деяким заданим квадратичним критерієм якості. Також ця теорія бере до уваги наявність збурень у вигляді гауссовського білого шуму. Однак незважаючи на те, що синтез ЛКГ-контролерів передбачає систематичну процедуру розрахунку для оптимізації якості системи, головним його недоліком є те, що в розгляд не приймається робастність системи. Тому ЛКГ-синтез проводиться тільки для систем, що мають надійну і точну лінійну динамічну модель. Для підвищення робастності системи управління застосовують більш складні алгоритми, такі як мінімаксний ЛКГ синтез, або комібінованний ЛКГ синтез. ЛКГ контролери можуть використовуватися як для дискретних, так і для безперервних систем.

Лінійний квадратичний Гауссівський (LQG) регулятор – сучасний метод синтезу оптимальних динамічних регуляторів у просторі станів. Такий регулятор складається з матриці оптимальних коефіцієнтів зворотних зв’язків за змінними стану та естиматора на основі фільтра Калмана.Такий регулятор описується векторно – матричним рівнянням:

На першому етапі синтезу шукаються параметри зворотніх зв’язків за змінними стану, що мінімізують функціонал якості системи:

Матриця коефіцієнтів зворотніх зв’язків K отримується розв’язанням алгебраїчного рівняння Ріккаті:

S×A+A’×S-(S×B+N)×R^-1×(B’×S+N’)+Q=0

Отриманні значення коефіцієнтів підсилення називаються LQ- оптимальним підсиленням

На наступному кроці визначаються параметри естиматора координат простору стану для реалізації зворотніх зв’язків за змінними стану, які неможливо виміряти безпосередньо. Таким естиматором є фільтр Калмана.

Фільтр Калмана - ефективний рекурсивний фільтр, що оцінює вектор стану динамічної системи, використовуючи ряд неповних та зашумлених вимірювань. Названий на честь Рудольфа Калмана.

Фільтр Калмана широко використовується в інженерних та економетричних ужитках: від радарів і систем технічного зору до оцінок параметрів макроекономічних моделей. Калманова фільтрація є важливою частиною теорії управління, відіграє велику роль у створенні систем управління. Спільно з лінійно-квадратичним регулятором фільтр Калмана дозволяє вирішити задачу лінійно-квадратичного гауссівського управління. Фільтр Калмана і лінійно-квадратичний регулятор - можливе рішення більшості фундаментальних завдань в теорії управління.

У більшості ужитків, кількість параметрів, які задають стан об'єкта, більше, ніж кількість спостережуваних параметрів, доступних для вимірювання. За допомогою моделі об'єкта по ряду доступних вимірів фільтр Калмана дозволяє отримати оцінку внутрішнього стану.

Фільтр Калмана призначений для рекурсивної дооцінки вектора стану апріорно відомою динамічної системи, тобто для розрахунку поточного стану системи необхідно знати поточний вимір, а також попередній стан самого фільтра. Таким чином фільтр Калмана, як і безліч інших рекурсивних фільтрів, реалізований у часовому поданні.

На третьому кроці синтезу на основі одержаних даних з двох попередніх кроків формується LQG – регулятор.

У середовищі пакета Control System Toolbox ці операції виконуються за допомогою таких функцій:

· Сare – розв’язування рівняння Рікатті для неперервної системи.

· Dare – розв’язування рівняння Рікатті для дискретної системи.

· Dlqr – знаходить LQ-оптимальне підсилення для дискретної системи.

· Kalman – розраховує параметри естиматора.

· Kаlmd – параметри дискретного естиматора для неперервного об’єкта.

· Lqgreg – формує LQG регулятор на основі знайдених коефіцієнтів підсилення і параметрів фільтра Калмана.

· Lqr – знаходить LQ-оптимальне підсилення для неперервних систем.

· Lqrd – параметри дискретної системи керування для неперервного об’єкта.

Як приклад застосування методу синтезу LQG – регулятора, розглянемо задачу стабілізації показану на рис.8.1.

Рис.8.1 Задача стабілізації

Ціль керування полягає в тому, щоб регулювати вихід об’єкта Y біля нуля. На систему діє збурення типу білого шуму d та наявний деякий шум вимірювання n з такими шумовими властивостями:

E(d²)=1, E(n²)=0.01

Функціонал якості системи має вигляд

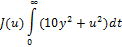
Розімкнута модель системи в просторі станів.

Де (A, B, C) – реалізація моделі в просторі станів системи, що описується передавальною функцією 100/(s²+s+100).

Наведенні нижче команди синтезують оптимальний LQG – регулятора для сформульованої задачі:

%модель об’єкта в просторі станів

sys = ss(tf(100,[1 1 100]));

%визначення коефіцієнта К

K = lqry(sys,10,10); % u = -Kx мінімізує J(u)

%Розділення входу керування u і входу збурення d

[A, B, C, D] = ssdata(sys);

P = ss(A, [B,B], C, [D, D]); % вхід [u; d], вихід y

% Розробка естиматора стану KEST

Kest = kalman(P,1,0.01);

% Формування LQG регуляторa = LQ підсилення + фільтр Калмана

F = lqgreg(Kest,K);

На рис.8.1 зображено реакцію розімкненої і замкненої за допомогою синтезованого регулятора систем на одиничний імпульс.

% Формування замкнутої системи

clsys = feedback(sys,F,+1) % додатній зворотній зв’язок

clsys_fin = clsys;

% Реакція розімкненої і замкненої систем на одиничний імпульс

impulse(sys,'r--',clsys_fin,'b-')

Рис.8.2 Результат імітаційного моделювання

Поиск по сайту: