Понятие устойчивости

Понятие устойчивости системы характеризует способность возвращаться в состояние равновесия (или заданного движения) после прекращения действия внешних сил, которые вывели ее из этого состояния.

Устойчивость положения равновесия.

Пусть у * — положение равновесия, а y (t) — текущее значение координаты (процесса). Положение равновесия называется устойчивым, если рассогласование D y (t) = y (t) - y * с течением времени будет стремиться к нулю. Ниже представлена механическая аналогия (рис. 2.34).

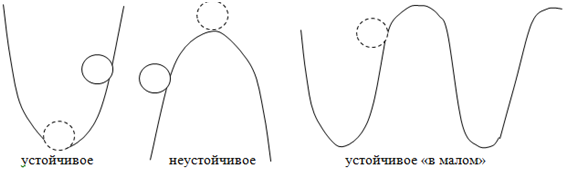
Рис. 2.34. Положение равновесия

Если устойчивость положения равновесия наблюдается при любых начальных условиях, то говорят об устойчивости «в большом». Под устойчивостью «в малом» понимается соблюдение условия D y (t) ® 0 при t ® ¥ в малой e-окрестности положения равновесия.

Понятие устойчивости можно распространить и на случай движения. Пусть заданное (невозмущенное) движение определяется законом y *(t). Приложение внешних сил к системе вызовет отклонение действительного (возмущенного) движения (рис. 2.35) от заданного: y ^(t) ¹ y *(t).

Заданное невозмущенное движение будет устойчивым, если возникающее в результате приложения внешних сил возмущенное движение по истечении некоторого времени после снятия этих сил будет стремиться к заданному (т. е. система выйдет на прежнюю траекторию): D y (t) = y (t) – y *(t) ® 0 при t ® ¥.

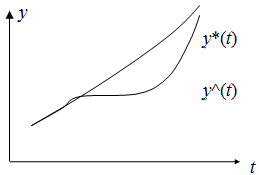
Рис. 2.35. Возмущенное движение

Исследование устойчивости «в большом» является предметом теории нелинейных систем. Устойчивость «в малом» исследуется на линеаризованных моделях. В линейных системах свойство устойчивости от величины внешних воздействий не зависит. Не зависит устойчивость линейных систем и от начальных условий. Устойчивость является внутренним свойством системы и определяется только ее параметрами.

Рассмотрим линейную систему, описываемую дифференциальным уравнением:

a ₀ y ⁽ⁿ⁾ + a ₁ y ^{(n -1)} + a ₂ y ^{(n -2)} +...+ a_ny = b ₀ x ^(m) + b ₁ x ^{(m -1)} + +...+ b_mx (2.49)

Невозмущенное движение является одним из возможных, поэтому

a ₀ y* ⁽ⁿ⁾ + a ₁ y* ^{(n -1)} + a ₂ y* ^{(n -2)} +...+ a_ny* = b ₀ x ^(m) + b ₁ x ^{(m -1)} +...+ b_mx (2.50)

Вычитая (2.49) – (2.50), получим для определения D y (t) (а значит и для исследования устойчивости) линейное однородное дифференциальное уравнение с постоянными коэффициентами:

a ₀D y ⁽ⁿ⁾ + a ₁D y ^{(n -1)} + a ₂D y ^{(n -2)} +...+ a_n D y = 0 (2.51)

Решение уравнения имеет вид D y (t) = S С_iexp (l _it) и для определения l _i следует решить уравнение

Q (l) = a ₀l ⁿ + a ₁l ^{n -1} + a ₂l ^{n -2} +...+ a_n = 0 (2.52)

Это уравнение называется характеристическим уравнением системы, а полином Q (l) называется характеристическим полиномом системы.

Коэффициенты С_i — постоянные, определяемые начальными условиями. Для устойчивости системы при любых начальных условиях (для любых С_i) должно выполняться условие D y (t) ® 0
при t ® ¥, а значит необходимо выполнение требования Re l _i < 0.

Итак, необходимое и достаточное условие устойчивости системы: все корни характеристического уравнения должны иметь отрицательную вещественную часть.

На практике для исследования устойчивости вместо решения характеристического уравнения и определения знаков его корней используют критерии устойчивости: алгебраические и частотные.

Критерии устойчивости – это некие правила, позволяющие судить об устойчивости систем. Алгебраические критерии устойчивости используют для этой цели значения коэффициентов характеристического уравнения системы, частотные критерии — частотные характеристики.

Поиск по сайту: