 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Виды особых точек
Рассмотрим особую точку – решение системы уравнений (5.4). Пусть функции f 1 и f 2 в окрестности этой точки допускают разложение в степенной ряд по отклонениям переменных (D х 1, D х 2). Тогда вместо нелинейных уравнений (5.2) можно получить систему линейных дифференциальных уравнений для малых отклонений переменных, которая в матричной форме примет вид:
| (5.8) |

A – матрица Якоби системы (5.2) в рассматриваемой точке равновесия.
Решения уравнений (5.8) имеет вид:
| (5.9) |
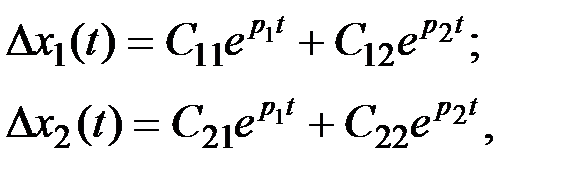
| (5.10) |
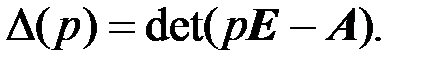
Рассмотрим типы особых точек линейных систем второго порядка, в зависимости от расположения корней характеристического полинома (5.10), т. е. собственных значений матрицы A.
1. ЦЕНТР – корни чисто мнимые
Чисто мнимым корням консервативной системы р 1,2 = ± i w0 соответствует особая точка типа “центр” и фазовые траектории, образованные вложенными друг в друга эллипсами (рис. 5.6). Незатухающий колебательный процесс гармонической формы с периодом T = 2p/w0 имеет амплитуду, определяемую начальными условиями.
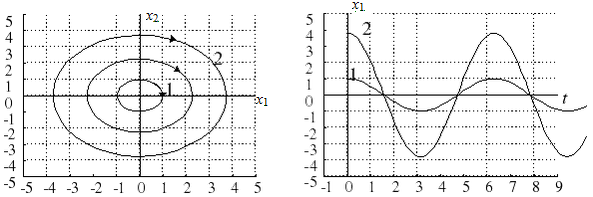
Рис. 5.6 – Особая точка типа “центр”
Получим уравнение фазовых траекторий для этого случая на примере дифференциального уравнения
| (5.11) |
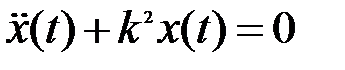
с начальными условиями
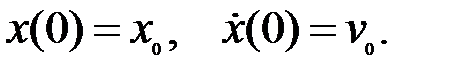
Характеристическое уравнение имеет вид
| (5.13) |
| (5.12) |
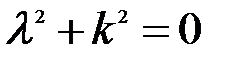 .
.
Корни характеристического уравнения
 .
.
Решение дифференциального уравнения (5.11) имеет вид
| (5.15) |
| (5.14) |

где с 1 и с 2 – постоянные интегрирования, которые определяются заданными начальными условиями.
Вычислим постоянные интегрирования. Для этого определяем производную 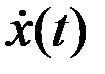

Теперь используем заданные начальные условия
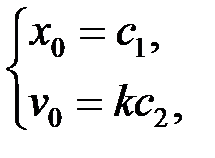
откуда
| (5.16) |
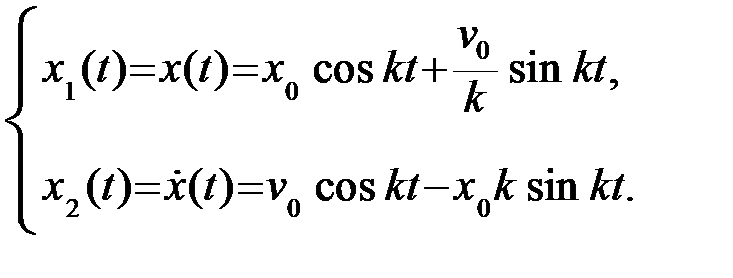
Для того, чтобы получить уравнение фазовых траекторий, нужно из уравнений (5.16) исключить время t.
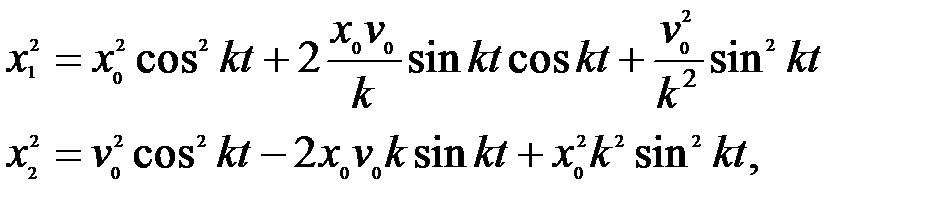
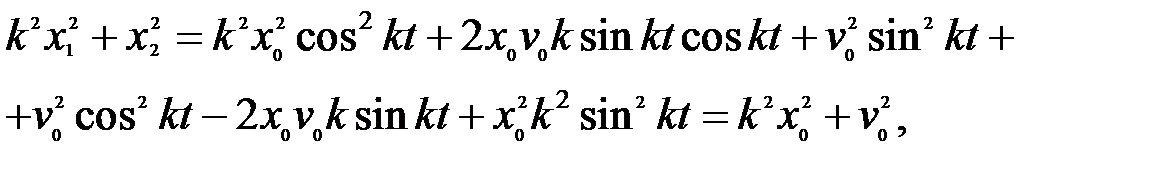
| (5.19) |
| (5.18) |
| (5.17) |
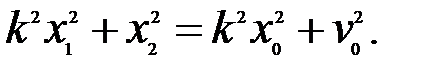
или

Таким образом, фазовые траектории – это эллипсы с центром в начале координат и полуосями 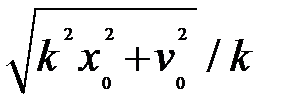 и
и 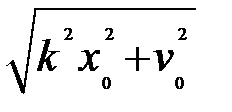 .
.
Можно фазовые траектории получить другим способом. Из уравнения (5.11) получим систему уравнений
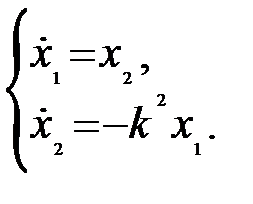
Разделим второе уравнение системы (5.19) на первое
| (5.20) |

Получили линейное дифференциальное уравнение с разделяющимися переменными. Решим это уравнение
| (5.21) |

где с – постоянная интегрирования.
Если определить постоянную с из заданных начальных условий  то получим уравнение (5.18).
то получим уравнение (5.18).
Вывод. Если корни характеристического уравнения являются чисто мнимыми числами  , то фазовые траектории представляют собой концентрические эллипсы с центром в начале координат, а особая точка – центр.
, то фазовые траектории представляют собой концентрические эллипсы с центром в начале координат, а особая точка – центр.
2. Устойчивый УЗЕЛ
Если корни p 1, p 2 полинома (5.10) действительные отрицательные, то имеет место особая точка типа “устойчивый узел” (рис. 5.7). Прямолинейным фазовым траекториям соответствуют состояния, когда постоянные при одной из экспонент (5.9) равняются нулю. Кривые 1 и 2 соответствуют различным начальным условиям.
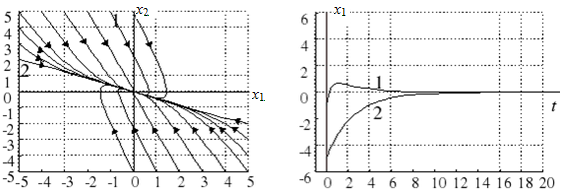
Рис. 5.7. Особая точка типа “устойчивый узел”
3. Неустойчивый УЗЕЛ
При положительных действительных корнях p 1, p 2 имеем особую точку типа “неустойчивый узел” (рис. 5.8).
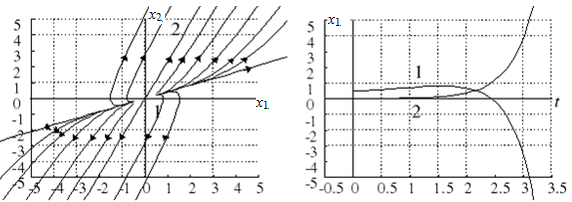
Рис. 5.8. Особая точка типа “неустойчивый узел”
4. СЕДЛО
Если один из действительных корней отрицательный, а другой – положительный, то особая точка называется “седло” (рис. 5.9). Прямолинейные траектории ― сепаратрисы седла ― соответствуют случаю, когда один из коэффициентов в (5.10) равен нулю.
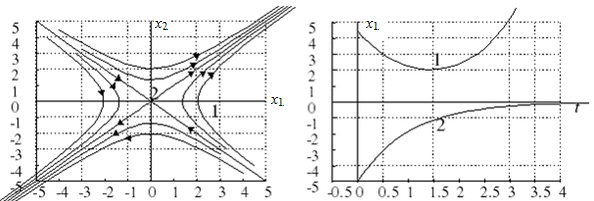
Рис. 5.9. Особая точка типа “седло”
5. Устойчивый ФОКУС
Комплексно-сопряженные корни с отрицательными действительными частями дают особую точку типа “устойчивый фокус” (рис. 5.10).
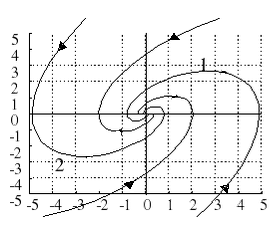
Рис. 5.10. Особая точка типа “устойчивый фокус”
6. Неустойчивый ФОКУС
Если действительные части комплексных корней положительны, то имеем “неустойчивый фокус” (рис. 5.11) и колебательные расходящиеся процессы.
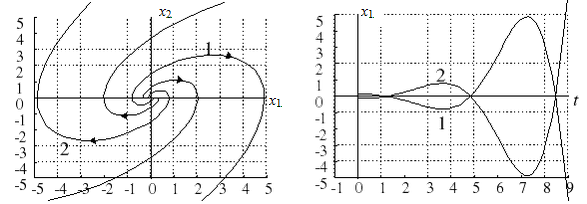
Рис. 5.11. Особая точка типа “неустойчивый фокус”
Особым точкам типа “устойчивый узел” и “устойчивый фокус” соответствуют устойчивые “в малом” положения равновесия нелинейной системы. В случае особых точек “седло”, “неустойчивый узел” и “неустойчивый фокус” положения равновесия неустойчивы. В случае особой точки типа “центр” об устойчивости положения равновесия нелинейной системы нельзя судить по линеаризованным уравнениям.
Поиск по сайту: