Количество движения системы материальных точек равно количеству движения массы всей системы, сосредоточенной в центре масс

2. Сумма моментов количества движения или кинетический момент системы:

.

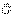представляется в виде одночлена только в случае одинаковых скоростей всех точек системы.

3. Кинетическая энергия системы:

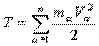
Тоже не всегда представлена в одночленной форме.

Силы разделим на внешние и внутренние.

Внешние силы действуют со стороны масс, не входящих в систему.

Внутренние силы – силы взаимодействия между точками системы.

Обозначим:

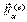- суммарная внешняя сила к точке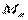

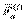- суммарная сила взаимодействия точки 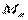c остальными точками системы.

Деление на внутренние и внешние силы условно.

Получим некоторые свойства внутренних сил.

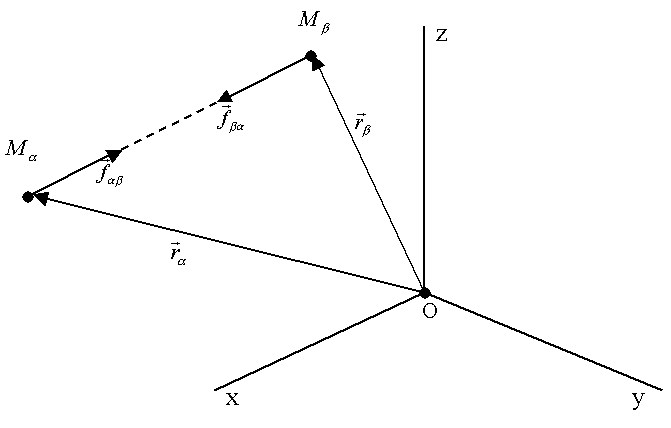
Рис.54.

Рассмотрим точки 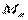и (рис. 54).

Из 3 – го закона Ньютона:

.

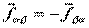Внутренняя сила на точку :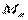

.

Очевидно:

.

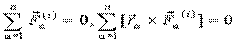Итак, сумма внутренних сил и сумма моментов внутренних сил равны нулю относительно любой точки и любой оси.

Рассмотрим сумму элементарных работ внутренних сил.

Пусть 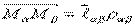, где ,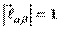

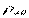- расстояние между точками .

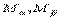Работа на элементарных действительных перемещениях сил взаимодействия двух точек :

.

[ - проекция на 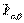, включающая в себя знак].

Обозначим сумму элементарных работ внутренних сил :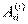

(d – означает «на элементарных перемещениях»)

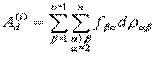
Контрольные вопросы:

1. Что называется центром масс системы материальных точек?

2. Назовите основные меры движения системы материальных точек.

3. Перечислите свойства внутренних сил системы точек?

Лекция 19. Общие теоремы динамики системы точек

Основные (общие) теоремы динамики систем свободных материальных точек являются уравнениями движения систем свободных материальных точек, т. е. математически дифференциальными уравнениями изменений основных мер движения.

1. Для точки уравнение движения относительно инерциальной системы отсчёта:

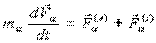
Перенесём все векторы, не изменяя их направления, в центр масс и сложим геометрически:

.

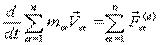Производная по времени от количества движения системы свободных материальных точек равна геометрической сумме внешних сил. Это теорема об изменении количества движения системы.

Так как 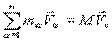то

.

Это уравнение движения центра масс системы материальных точек с массой, равной массе всей системы, к которой приложена сумма всех внешних сил (главный вектор внешних сил) или теорема о движении центра масс.

2. Умножим уравнение движения точки слева векторно на и геометрически сложим, перенося векторы в центр масс:

.

Теорема об изменении кинетического момента системы:

Поиск по сайту: