 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кинематика точки. Декартовы координаты
С неподвижной системой отсчёта связываем декартовую ортогональную систему координат (правую, рис. 31).
Рис.31.
Точка 
, где
– параметрические уравнения траектории.
где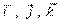 
- единичные векторы (орты),
- непрерывны и 2 раза дифференцируемы; 2-е производные – непрерывны.
Непрерывная последовательность точек среды (пространства), занимаемая точкой M, называется траекторией точки М.
Исключая время:
или:
Введём понятия скорости и ускорения:
Рис.32.
т. М 
t
т. М’ t + t
( t - конечное).
Радиусы – векторы: t 
t + t +
= 
За время t (рис. 32):
(Направление по секущей MM’).
Скорость точки в момент времени t получается при t 0, то есть
(Направление по касательной и траектории точки)
Очевидно:
Проекции 
:
.
Модуль (длина):
Скорость точки М в момент времени t равна производной по времени от радиуса – вектора точки и направлена по касательной к траектории.
Аналогично найдём ускорение (рис. 33).
Рис.33.
Совмещая начало векторов 
(t) и (t + t) в точке М => за t.
Среднее ускорение:
(направление в сторону вогнутости траектории)
Ускорение точки в момент времени t получается при t 0, то есть
Очевидно:
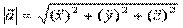
Ускорение точки в некоторый момент времени равно производной по времени от вектора скорости, или второй производной по времени от радиуса – вектора точки в этот момент времени.
В некоторых задачах – используется производная более высоких порядков, но здесь они пока не нужны.
В механике применяются не только декартовы координаты – часто применяют обобщённые (криволинейные) координаты.
Они бывают удобней, позволяют определить конфигурацию рассматриваемой системы. Часто их называют позиционными. Криволинейными они называются потому, что линии вдоль которых меняется только одна координата, обычно бывают кривыми.
Рассмотрим частный случай криволинейных координат – полярные координаты точки на плоскости: применим далее к задаче движение точек в центральном силовом поле (рис. 34).
Рис.34.
(x, y) – декартовы координаты.
(r,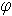 
) – полярные координаты.
Угол 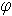=> от Ох против часовой стрелки – положительное направление
Формулы преобразования:
x = r cos 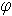, y = r sin 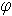, где r 
0; 0 
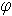< 2 
(можно рассматривать и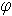 
).
Если r = const – концентрические окружности с центром в точке О.
Если 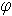= const – прямолинейные лучи из точки О.
Введём два орта:
Найдём производные 
по углу 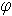(рис. 35):
Рис.35.
(так как r = 1)
при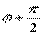 
,
т. е. 
.
Далее:
при ,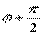
т. е. 
.
При каждом дифференцировании по φ т. е. происходит поворот на угол 
.
Выведем формулы проекции скорости и ускорения точки М на направления касательных к координатным линиям в полярных координатах.
Так как 
, то
Но: 
Очевидно:
Для ускорения:
.
Но: 
.
Очевидно:
Контрольные вопросы:
1. Что изучает кинематика?
2. Дайте определение скорости точки.
3. Напишите формулы проекций ускорения на оси полярной системы координат.
Лекция 9. Естественные координаты
Рассмотрим систему координатных осей, определяемую траекторией точки (рис.36).
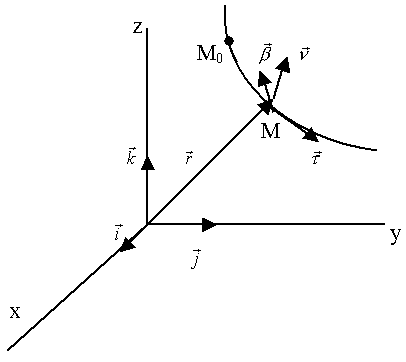
Рис.36.
.
Единичный вектор касательной к траектории (S – длина дуги М0М):
, где 
.
Дифференцируя 
по S: 
,
где 
- единичный вектор главной нормали; 
и направлен в сторону вогнутости;
кривизна. (k = 0 - прямая); 
- радиус кривизны.
Единичный вектор бинормали 
:
.
образуют правую тройку ортогональных единичных векторов. Они определяют направление естественных (натуральных) осей в том месте траектории, где находится движущаяся точка.
соприкасающаяся 
Очевидно, проекция на ось 
: 
(может иметь разные знаки – зависит от направления S).
Для ускорения:
;
Но: 
;
Очевидно, проекции ускорения на естественные оси:
на касательную: 
;
на главную нормаль: 
на бинормаль: 0
Таким образом, ускорение лежит в соприкасающейся плоскости (рис. 37).
Рис.37.
Поиск по сайту: