Кинематика зубчатых механизмов с неподвижными осями вращения

Для получения больших передаточных отношений применяются многоступенчатые передачи, составленные из нескольких простых зубчатых передач. Рассмотрим трехступенчатую передачу.

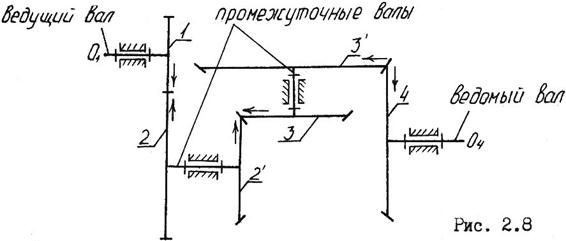
Передаточное отношение всего механизма равно

(2.2)

апередаточное отношение отдельных ступеней –

Перемножим эти отношения:

(2.3)

Сравнивая выражения (2.2) и (2.З), получим

т.е. передаточное отношение многоступенчатой передачи равно про­изведению передаточных отношений отдельных ступеней.

Колеса 1 и 4 вращаются в одну сторону. Таким образом,

Если все ступени являются цилиндрическими передачами, то в общем случае

(2.4)

где n - число внешних зацеплений.

Частным случаем многоступенчатой передачи является ступенчатый ряд с промежуточными (па­разитными) колесами (рис.2.9).

Промежуточные колеса не влияют на величину общего передаточного отношения, но могут изме­нять его знак. Такие передачи применяются для изменения направления вращения ведомого звена, а также в случае передачи вращения между уда­ленными валами. В общем случае

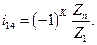(2.5)

2.4. Кинематика зубчатых механизмов с подвижными осями вращения

К механизмам с подвижными осями относятся механизмы, в со­ставе которых имеется хотя бы одно колесо с перемещающейся в пространстве осью вращения (сателлит). Различают три вида таких механизмов:
1) дифференциальные, 2) планетарные, 3) замкнутые дифференциальные.

Рассмотрим один из простейших дифференциальных механизмов (рис.2.10).Звенья 1 и 3 – центральные колеса, 2 – сателлит, Н –водило. Водило Н и соосные с ним центральные колеса 1 и 3 назы­ваются основными звеньями.

Получим формулу, связывающую угловые скорости звеньев в дифференциальном механизме. Используем метод обращения движения. Сообщаем всем звеньям механизма дополнительную угловую скорость, равную угловой скорости водила Н, но противоположно направленную, т.е. (). При этом относительное движение звеньев не изме­нится, а угловые скорости в обращенном движении будут следующи­ми:

Таким образом, так как то дифференциальный меха­низм превратился в зубчатый механизм с неподвижными осями. Для такого обращенного механизма

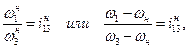(2.6)

где 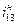- передаточное отношение обращенного механизма, опре­деляемое через число зубьев колес:

Полученное выражение(2.6) называется формулой Виллиса. В общем случае формула Виллиса имеет вид

Если в дифференциальном механизме одно из центральных ко­лес сделать неподвижным, то получится планетарный механизм (рис. 2.11).

Так как то из формулы

получим:

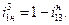(2.7)

Выражение(2.7) называется формулой Виллиса для планетарных механизмов. В общем случае она имеет вид

(2.8)

где индекс в соответствует неподвижному центральному колесу.

Планетарные механизмы часто называются планетарными пере­дачами. Они позволяют получать большие передаточные отношения при малых габаритах.

Пример. Определить если (рис.2.12).

На основании формулы (2.7) находим

Поиск по сайту: