Синтез систем управления методом логарифмических частотных характеристик

Одним из основных, наиболее часто используемых методов синтеза линейных систем является метод, основанный на использовании асимптотических логарифмических частотных характеристик разомкнутой системы. С одной стороны, свойства системы автоматического управления полностью определяются частотными характеристиками ее разомкнутого контура, с другой стороны, эти характеристики легко строятся.

Этот метод может быть применен даже тогда, когда неизвестны передаточные функции отдельных элементов. В этом случае используются экспериментально снятые частотные характеристики указанных элементов или разомкнутой системы в целом.

Исходными данными при проектировании являются передаточная функция G (p) объекта без регулятора (располагаемой системы) или экспериментально снятые частотные характеристики объекта и желаемые требования к объекту:

- коэффициенты ошибок регулирования по положению, скорости и производным высших порядков;

- время переходного процесса t _пп;

- перерегулирование s;

- запасы устойчивости по амплитуде D A и фазе Dj.

Методика синтеза последовательного регулятора по логарифмическим частотным характеристикам включает в себя следующие этапы:

· построение асимптотических ЛЧХ располагаемой системы;

· построение асимптотических ЛЧХ желаемой разомкнутой системы (рис. 3.8);

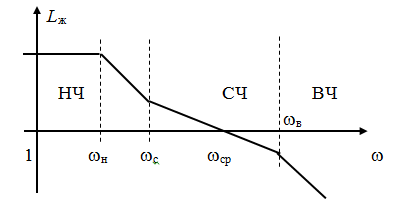
Рис. 3.8. Желаемая ЛАХ

· определение асимптотических ЛЧХ регулятора;

· построение передаточной функции регулятора;

· построение переходной характеристики синтезированной замкнутой системы;

· проверка соответствия полученной системы заданным требованиям;

· техническая реализация регулятора.

Блок-схема алгоритма синтеза представлена на рис. 3.9.

начало

G (p) D A, Dj,

s, t _пп, c_{i …}

L _р(w)= L _ж(w)– L (w)

j_р(w)=j_ж(w)–j(w)

R (p)

h (t), L (w)

св-ва достигнуты?

техническая реализация

регулятора

конец

Рис. 3.9. Блок-схема алгоритма синтеза регулятора методом ЛАХ

Методика синтеза последовательного регулятора основана на соотношениях

в которых индекс «ж» обозначает желаемые передаточную функцию и частотные характеристики разомкнутого контура, и на зависимости свойств замкнутой системы от характеристик разомкнутой.

Характеристики регулятора получают путем графического вычитания

L _р(w) = L _ж(w) – L (w), j_р(w) = j_ж(w) – j(w).

Передаточную функцию регулятора R (p) восстанавливают по его частотным характеристикам.

На первом этапе строятся асимптотические логарифмические частотные характеристики L (w) и j(w), соответствующие передаточной функции G (p) разомкнутой системы (располагаемой, без регулятора). Построение может быть выполнено теоретическими методами на основе математической модели или экспериментально.

Наиболее сложным является второй этап формализации желаемых свойств замкнутой системы в форме желаемых логарифмических частотных характеристик L _ж(w) и j_ж(w) разомкнутой системы. Их формирование выполняется по-разному в разных частотных диапазонах.

Низкочастотная часть желаемой амплитудной характеристики в интервале частот 0 £w £ w_н должна иметь наклон 0 или –20∙ m дБ/дек, где m – требуемая степень астатизма системы, и отсекать на оси L желаемое значение L_ж (1), определяемое по общему коэффициенту усиления желаемой разомкнутой системы. Подробнее об определении этого коэффициента, а также других параметров желаемой характеристики речь идет ниже.

Среднечастотная часть желаемой амплитудной характеристики в интервале частот w_с £ w £ w_в должна иметь наклон –20 дБ/дек (или в отдельных случаях –40 дБ/дек) и пересекать ось w на желаемой частоте среза w_ср.

Низко- и среднечастотная части амплитудно-частотной характеристики соединяются в интервале частот w_н < w < w_с сопрягающей частью c наклоном –40 дБ/дек или –60 дБ/дек.

Высокочастотная часть желаемой амплитудной характеристики при w > w_в должна иметь отрицательный наклон от –40 дБ/дек и более, так как она предназначена для максимального ослабления влияния высокочастотных шумов на работу системы управления (а для этого должна быстро убывать по величине с увеличением частоты).

При формировании желаемой амплитудно-частотной характеристики необходимо стремиться максимально совмещать частоты сопряжения асимптотических характеристик L (w) и L _ж(w), чтобы упростить структуру регулятора, исключив лишние типовые звенья в его передаточной функции R (p) = G _ж(p)/ G (p).

На третьем этапе графическим вычитанием

L _р(w) = L _ж(w) – L (w), j_р(w) = j_ж(w) – j(w)

определяются логарифмические характеристики последовательного регулятора. Эта операция выполняется достаточно просто, так как на отдельных участках сводится к вычитанию углов наклона прямых, кратных 20 дБ/дек.

По этим характеристикам на четвертом этапе восстанавливаются типовые звенья и передаточная функция регулятора R (p) по следующей методике:

· начальному низкочастотному участку характеристики L _р(w) с наклоном асимптоты ±20 m ₀ дБ/дек соответствует начальное типовое звено с передаточной функцией Коэффициент усиления определяем по координате L _р(1), отсекаемой на оси L низкочастотной асимптотой графика L _р(w) или ее продолжением;

· двигаясь слева направо по оси w, фиксируем частоты сопряжения w _i асимптотической амплитудной характеристики L _р(w). Каждому изменению ее наклона на ±20 дБ/дек соответствует типовое звено регулятора с передаточной функцией

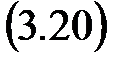
(символ Å означает знак «+» для минимально-фазовых звеньев и знак «–» – для неминимально-фазовых).

· составляем из типовых звеньев R_i (p) передаточную функцию регулятора

На пятом этапе проектирования регулятора получают фактические показатели качества замкнутой системы путем вычисления ее передаточной функции G _ж(p) и построения переходной характеристики

На шестом этапе статические и динамические свойства переходной характеристики сравниваются с желаемыми.

Если в процессе проектирования желаемые свойства замкнутой системы достигнуты, то на седьмом этапе выполняется техническая реализация полученной передаточной функции регулятора:

• последовательный регулятор преобразуется к желаемому типу или к комбинации регуляторов разных типов;

• разрабатывается техническое устройство, реализующее регулятор в требуемой элементной базе.

Если требуемые свойства замкнутой системы не достигнуты, желаемые логарифмические частотные характеристики корректируются, а цикл проектирования повторяется со второго этапа.

Главные достоинства расчета регулятора методом логарифмических частотных характеристик заключаются в использовании кусочно-линейных асимптотических характеристик, которые легко и быстро строятся по передаточной функции и так же быстро позволяют восстановить передаточную функцию по логарифмическим характеристикам. Применение номограмм позволяет исключить решение нелинейных уравнений для определения параметров желаемой ЛАХ.

Пример. Для объекта с передаточной функцией

рассчитать последовательный регулятор, дающий замкнутой системе астатизм первого порядка с предельной ошибкой отработки заданного линейного сигнала, не превышающей 10 % скорости его изменения, показателями качества t _пп £ 2 с, s £ 20 % и запасами устойчивости
D А ³ 6 дБ и Dj ³ p/4.

Решение. Сначала строим асимптотические логарифмические характеристики объекта L (w) и j(w) (рис. 3.10). Затем сформируем желаемую ЛАХ (L _ж).

Рис. 3.10. Логарифмические частотные характеристики

· Начальный участок желаемой асимптотической ЛАХ имеет наклон –20 дБ/дек, так как система должна быть астатической.

· Установившаяся ошибка отработки линейного сигнала x (t) = x ₀ + vt равна e _уст(t) = c ₀(x ₀ + vt) + c ₁ v. Так как система астатическая, то c ₀ = 0. Из условия e _уст(t) £ 0,1 v следует e _уст(t) = c ₁ v £ 0,1 v Þ c ₁ £ 0,1. Отсюда получаем требование на выбор общего коэффициента усиления разомкнутой системы

c ₁ = 1/ К Þ К = 1/ c ₁ ³ 10 Þ L _ж(1) ³ 20 дБ.

· Влево от точки (1, 20) проводим пунктиром низкочастотную асимптоту амплитудной характеристики с наклоном –20 дБ/дек.

· Частота среза w_ср выбирается по заданным показателям качества переходного процесса t _пп и s с помощью номограмм t _ппw_ср(Р_mах / Р ₀) и s(Р_mах / Р ₀), (рис. 3.11).

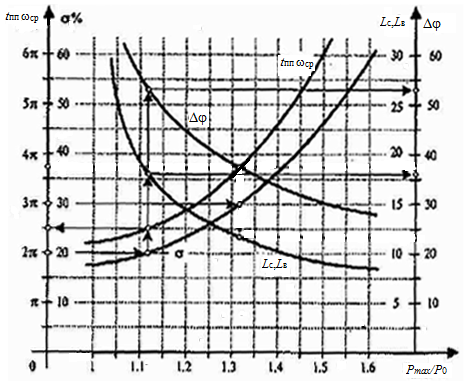
Рис. 3.11 – Номограммы для определения характеристик

Р_mах и Р ₀ – максимальное и начальное значения вещественной частотной характеристики замкнутой системы Р _з(w) = Re G _з(i w), задающие аргумент Р_mах / Р ₀, имеющий вспомогательный характер.

Последовательность применения номограмм показана стрелками:

• по желаемому перерегулированию s(%) находим аргумент Р_mах / Р ₀ и соответствующее ему произведение t _пw_ср времени переходного процесса t _п на частоту среза w_ср;

• деля это произведение на желаемое время переходного процесса t _пп (с), получим частоту среза w_ср;

• по номограммам Dj(Р_mах / Р ₀) и L _с, L _в(Р_mах / Р ₀) оцениваются запас устойчивости по фазе Dj (запас по амплитуде полагается равным 6 дБ) и минимальные значения краевых амплитуд L _с = L _ж(w_с) и
L _в = L _ж(w_в). Из соотношений

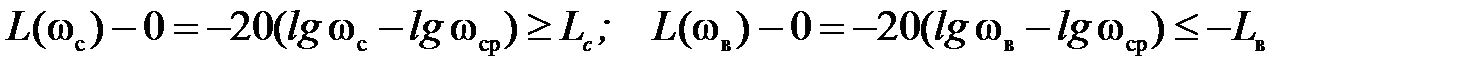
можно определить границы среднечастотного диапазона:

.

· По номограммам для s = 20% определяем произведение
t _ппw_ср »2,5p»8, а по нему частоту среза w_ср = 2,5p/ t _пп» 4 1/с.

· Через точку (w_ср, 0) проводим среднечастотную асимптоту также с наклоном –20 дБ/дек. По номограмме определяем минимальные значения амплитуд L _с = L _в » 16 дБ и границы среднечастотного диапазона:

· Так как низкочастотная и среднечастотная части L_ж (w) не пересекаются, то нужна сопрягающая часть с наклоном –40 дБ/дек. Чтобы выражение для передаточной функции регулятора (а значит и сам регулятор) было проще, следует, по возможности, совмещать сопрягающие частоты желаемой ЛАХ с сопрягающими частотами ЛАХ объекта. Поэтому совместим левую границу w_н характеристики L _ж(w) с частотой сопряжения асимптоты амплитудной характеристики объекта w₂ = 0,1 1/с. Тогда сопрягающая и среднечастотная асимптоты пересекутся на частоте w_c = 0,25 1/с Þ Т _c = 4 с, что удовлетворяет условию на w_c.

· Выберем частоту w_в = 40 1/с > 30 1/с сопряжения среднечастотной и высокочастотной асимптот желаемой амплитудной характеристики L_ж (w), откуда Т _в = 0, 025 с.

· По асимптотическим характеристикам L_ж (w), j _ж (w) восстановим передаточную функцию желаемого разомкнутого контура

· Рассчитаем реальные показатели качества полученной замкнутой системы по переходной характеристике

Эта характеристика имеет апериодический характер, перерегулирование s = 2,8% < 20%, быстродействие t _пп = 0,6 с < 2 с и нулевую статическую ошибку e_уст = 0 (рис. 3.12).

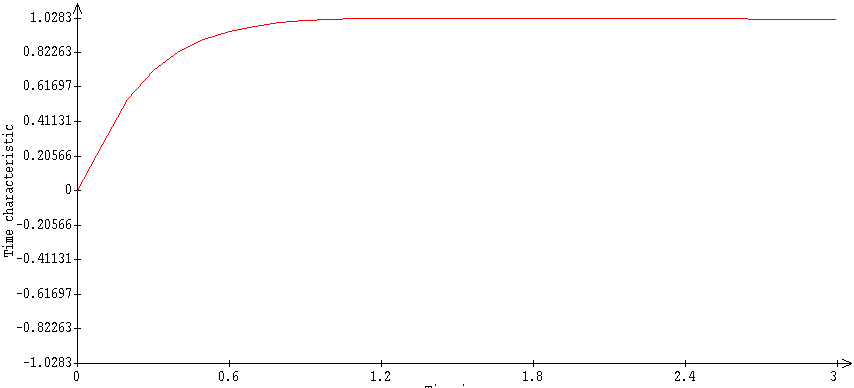
Рис. 3.12. Переходная характеристика желаемой системы

По логарифмическим частотным характеристикам желаемого разомкнутого контура определяем запас устойчивости по фазе
Dj > p/4.

Желаемые свойства замкнутой системы достигнуты. Вычисляем коэффициент статического усиления K _p = K _ж /K = 0,05 и передаточную функцию последовательного регулятора

Теперь можно сконструировать принципиальную схему корректирующего устройства на операционных усилителях (рис. 3.13).

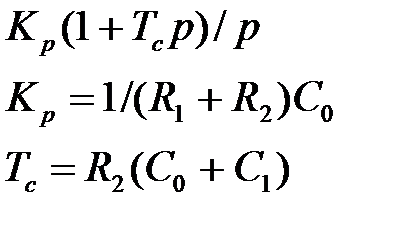
Рис. 3.13. Принципиальная схема корректирующего устройства

Для первого усилителя:

Для второго усилителя:

Для третьего усилителя:

Поиск по сайту: