Передаточная функция импульсной системы

Блок-схема разомкнутой импульсной системы, содержащей импульсный элемент (ИЭ), изображена на рис. 4.7. Реальный импульсный элемент обычно рассматривают как совокупность идеального импульсного элемента (ИИЭ) и непрерывного звена (формирующего элемента ФЭ, экстраполятора). Понятие идеального импульсного элемента можно ввести по-разному.

Рис. 4.7. Блок-схема разомкнутой импульсной системы

Можно считать, что идеальный импульсный элемент генерирует решетчатую функцию с периодом Т, образованную из непрерывного значения входного сигнала х (t): x (n) = х (t)| _t=nT. Подобным образом работают, например, устройства дискретного съема информации с объектов различного вида. Далее решетчатая функция x (n) поступает на формирующее устройство, а затем сигнал с выхода экстраполятора поступает собственно на непрерывную часть системы. Задача формирующего устройства заключается в формировании реального импульса прямоугольной, трапецеидальной, треугольной и т. п. формы. Совокупность идеального импульсного элемента и экстраполятора образует реальный импульсный элемент.

Можно ввести понятие идеального импульсного элемента и иначе, считая, что он генерирует с периодом Т последовательность импульсов типа d-функции, площади которых пропорциональны сигналу х (t) в моменты времени t = nT, т. е. x (n) = x (t)∙d(t–nT).

Введем понятие приведенной весовой функции g _п(t), понимая под этим термином реакцию непрерывной части системы (собственно непрерывная часть плюс формирующий элемент) на единичную импульсную решетчатую функцию d₀(n), где d₀(n) = 1 при n = 0 и d₀(n) = 0 при n ¹ 0. Согласно альтернативному определению идеального импульсного элемента, можно считать, что приведенная весовая функция g _п(t) является реакцией непрерывной части системы на d-импульсное входное воздействие, т. е. на сигнал d(t). По определению весовой функции для непрерывных систем это означает, что введенная функция g _п(t) как раз и является весовой функцией всей непрерывной части рассматриваемой амплитудно-импульсной системы.

Если выходную величину рассматривать только в дискретные моменты времени t = nT или t = (n +e) T, то система будет представлять собой импульсный фильтр. Он может характеризоваться приведенной решетчатой весовой функцией g _п(n) или смещенной решетчатой функцией g _п(n +e), полученной из производящей функции g _п(t). Другими словами, приведенная решетчатая весовая функция g _п(n) – это реакция g _п(t) непрерывной системы на импульсное входное воздействие d(t) в моменты времени t = nT.

Зная решетчатую весовую функцию g _п(n) или g _п(n +e), можно найти реакцию импульсного фильтра на входной сигнал произвольного вида.

Произвольный входной сигнал, поступающий на вход импульсного элемента в дискретные моменты замыкания ключа, можно представить в виде решетчатой функции с ординатами x (0)∙d(t), x (1)∙d(t – T), x (2)∙d(t –2 T), …, x (m)∙d(t – mT). Так как реакция непрерывной системы на сигнал d(t) равна g _п(t), то ее реакция на x (0)∙d(t) будет g _п(t)∙ x (0), на x (1)∙d(t – T) – g _п(t – T)∙ x (1), на x (m)∙d(t – mT) – g _п(t – mT)∙ x (m). Поэтому на выходе имеем .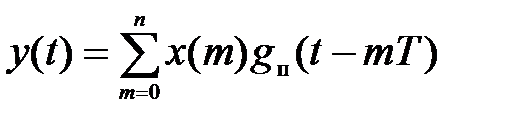

Таким образом, реакция импульсного фильтра, т. е. реакция непрерывной системы для дискретных моментов времени t = nT, равна

Найдем Z -преобразование от левой и правой частей последнего выражения (4.33). На основании формулы свертки где G (z) - есть Z -преобразование от приведенной решетчатой весовой функции,

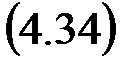
С другой стороны, по определению передаточной функции, где G (z) – дискретная передаточная функция системы. Следовательно, дискретная передаточная функция может быть определена как Z -преобразование от приведенной весовой функции.

Как найти функцию g _п(t) аналитически, по характеристикам элементов системы? Так как g _п(t) является весовой функцией приведенной непрерывной системы, то она связана с передаточной функцией G _п(p) этой системы соотношениями

Итак, дискретная передаточная функция должна определяться по приведенной весовой функции непрерывной части: сначала нужно определить передаточную функцию G _п(p) всей непрерывной части, включая формирующее звено, а только потом выполнять Z-преобразование.

Рассмотрим случай, когда в качестве формирующего звена используется экстраполятор с фиксацией на период (экстраполятор нулевого порядка). В этом случае на выходе экстраполятора в течение всего такта продолжительностью T удерживается величина, равная значению сигнала в момент начала такта (рис. 4.8). Подобным образом работают компьютерные и микропроцессорные системы управления.

Вычислим сначала изображение импульса на выходе экстраполятора

Рис. 4.8. Экстраполирование с фиксацией на период

Приведенная непрерывная система включает экстраполятор с передаточной функцией F ₀(p) и собственно непрерывную часть с передаточной функцией G _н(p). Передаточная функция приведенной непрерывной системы G _п(p) = F ₀(p) G _н(p). Тогда дискретная передаточная функция системы с экстраполятором нулевого порядка и собственно непрерывной частью, имеющей передаточную функцию G _н(p), будет равна

Пример. Определим дискретную передаточную функцию системы с экстраполятором нулевого порядка для случая, когда непрерывная часть имеет передаточную функцию .

Имеем 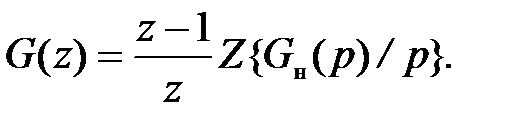Разложим выражение G _н(p)/ p на простые дроби:

Тогда из таблицы Z -преобразований найдем

Поиск по сайту: