 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Синтез для случая объекта, заданного передаточной функцией
Модель объекта представлена в форме передаточной функции
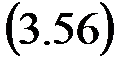
Этой передаточной функции соответствует дифференциальное уравнение
Введя обозначения x = x 1, далее получим
или в более компактной форме
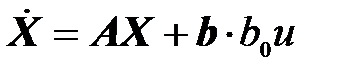
Здесь матрицы A и b уже имеют нормальную форму (3.51), т. е.
A = 
, b = 
, поэтому согласно (3.52) 
, а согласно (3.53) 
. Тогда на основании (3.54) имеем
Первое из равенств (3.61) означает, что в данном случае коэффициенты передачи модального регулятора сразу же могут быть вычислены по формулам (3.49). Последнее равенство в (3.61) означает, что на выходе такого регулятора последовательно с ним должен быть включен общий для всех каналов регулятора усилитель с коэффициентом усиления равным величине 
(это равноценно уменьшению всех расчетных коэффициентов регулятора в 
раз).
Подставив (3.61) в (3.60), получаем
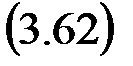
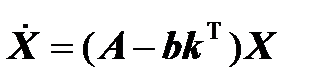
Для проверки решения следует, как и ранее, вычислить матрицу
G = A – bk T и определить ее характеристический полином.
Пример 2.Пусть объект представляет собой апериодическое звено второго порядка (рис. 3.23) с теми же значениями параметров. Отличие же состоит в том, что теперь доступной для управления является только одна выходная переменная объекта x 1.
Рис. 3.22. Структурная схема объекта
Требуется определить коэффициенты k, k 1, k 2, при которых “стандартный” характеристический полином модальной САУ имел бы ранее принятый вид
Q *(p) = p 2+ g 1 p + g 2 = p 2 + 6 p + 9.
Подобно (3.56) представим передаточную функцию объекта в следующей форме
Далее находим искомые коэффициенты
k = 1/ b 0 = 1/4;
=> 
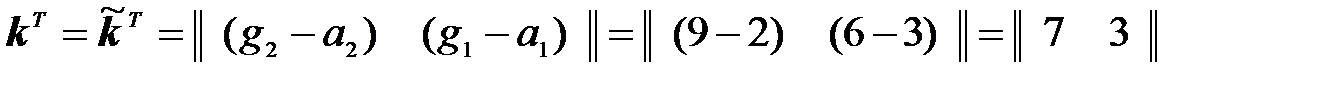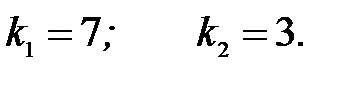
Таким образом, при тех же параметрах объекта, но измеряемой только одной из его переменных получили увеличенные, по сравнению с примером 1, значения коэффициентов модальных ОС.
Проверка.
Записываем матрицы объекта в нормальной форме
; 
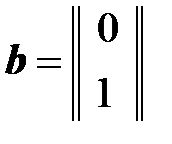
Далее вычисляем
и тогда
Полученный полином совпадает с ранее принятым “стандартным” характеристическим полиномом Q (p), следовательно, коэффициенты k 1, k 2 определены правильно.
Для определения коэффициента усилителя k y запишем коэффициент передачи всей системы и приравняем его к коэффициенту передачи самого объекта:
,
т. е. получили то же значение, как и в примере 1, что дополнительно подтверждает правильность вычисленных коэффициентов k, k 1, k 2.
Поиск по сайту: