 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Графо-аналитический синтез ПИД-регулятора
Алгоритм синтеза ПИД-регулятора включает следующие шаги.
1. Строятся логарифмические частотные характеристики объекта L (w) и j(w) (рис. 3.16), на оси ординат графика L (w) отмечается уровень (–DА), на оси ординат графика j(w) – уровень (jгр + Dj). Конкретные значения граничного уровня jгр = –p ± 2p n и знака Dj определяются по виду графика j(w) и желаемой характеристики jж(w).
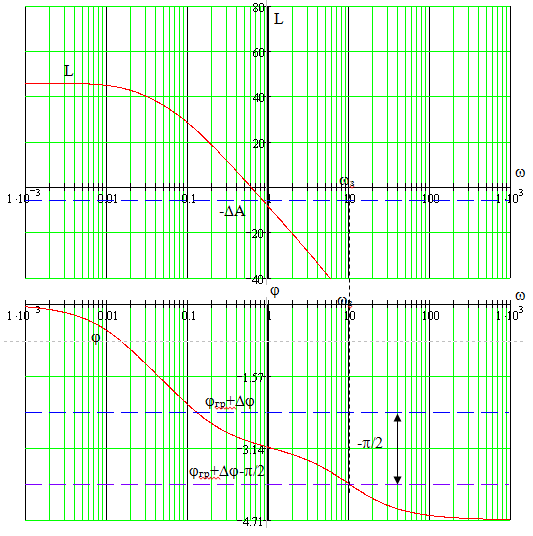
Рис. 3.16. Логарифмические частотные характеристики объекта
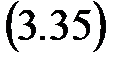 2. Вводится понятие частоты запаса wз желаемого разомкнутого контура согласно условиям:
2. Вводится понятие частоты запаса wз желаемого разомкнутого контура согласно условиям:
L ж(wз) = –DА, jж(wз) = jгр+Dj.
Для получения в замкнутой системе максимального быстродействия при сохранении запасов устойчивости эту частоту следует выбирать как можно большей.
С учетом подъема фазы, обусловленного дифференциальной составляющей регулятора на частотах w ³ 10 wд практически на p/2, нужную частоту ищут в точке пересечения графика j(w) с уровнем jгр + Dj – p/2, т. е. выбирают wз из условия
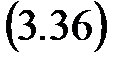 j(wз) = jгр + Dj – p/2.
j(wз) = jгр + Dj – p/2.
| L |
| w |
| w |
| L |
| j |
| -DA |
| wз |
| wз |
| -p/2 |
| j |
• если частота запаса wз существует, то принимают wд» 0,1wз Þ
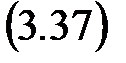 Т д» 10/wз.
Т д» 10/wз.
• если фазо-частотная характеристика объекта j(w) не достигает уровня jгр + Dj – p/2, то дифференциальный канал регулятора не обязателен (Т д = 0).
4. Строим частотные характеристики с учетом дифференциального канала (рис. 3.17)
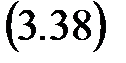
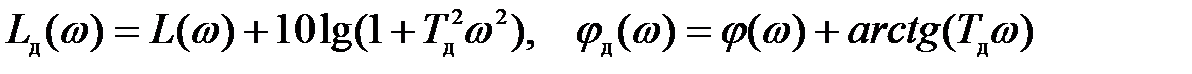
последовательного соединения объекта G (p) с форсирующим звеном (1+ Т д р) и визуально контролируем, чтобы фазовая характеристика jд(w) не входила в запретную зону (jгр + Dj; jгр) левее частоты wз. Если запас по фазе потерян, то следует интерактивно подбирать параметр wд (Т д) в окрестности значения wд» 0,1wз (Т д» 10/wз) до его восстановления.
| wд |
| w |
| w |
| L |
| L |
| Lд |
| wд |
| jд |
| j |
| j |
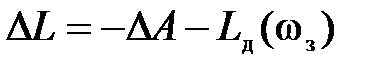 , определяем значение
, определяем значение 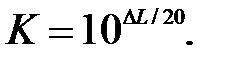 Затем строим характеристику
Затем строим характеристику 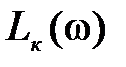 (рис. 3.18)
(рис. 3.18)
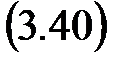
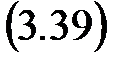
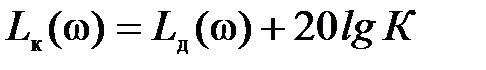 .
.
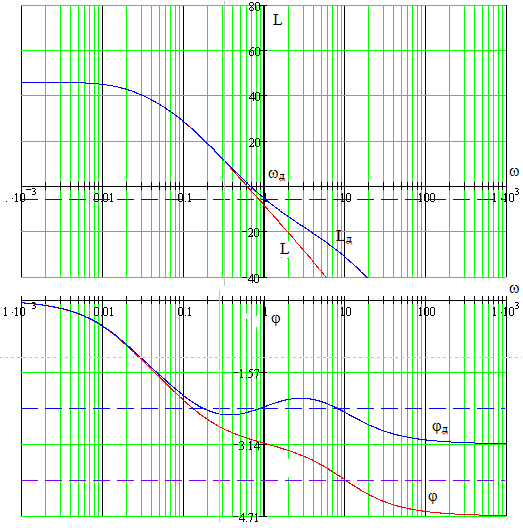
Рис. 3.17. Логарифмические частотные характеристики объекта с дифференцирующим (форсирующим) звеном
| K |
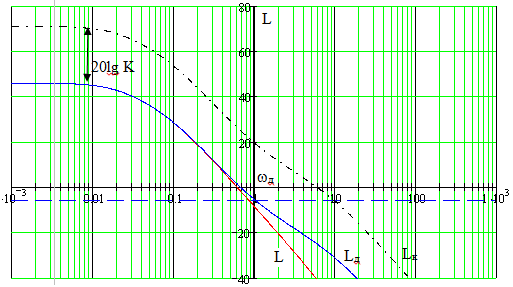
Рис. 3.18. Логарифмические частотные характеристики объекта с форсирующим звеном
| L |
| wд |
| Lк |
| Lд |
6. Теперь оценим значение частоты сопряжения изодромного звена wи. С одной стороны, при значении частоты равном wд, отрицательный фазовый сдвиг, вносимый изодромным звеном, должен уже закончиться, чтобы не нарушить запасы устойчивости, обеспечиваемые выбором wд (или, что то же самое Т д), и, следовательно, должно быть wи £ wд = wз/10. С другой стороны, чем выше wи, тем выше общий коэффициент усиления регулятора, а значит и разомкнутой системы в целом, что ведет к повышению точности замкнутой системы с регулятором (wи увеличивается с ростом К и). Таким образом, для достижения минимальной ошибки (коэффициента ошибки сn) частота wи должна располагаться как можно правее, не превышая, однако, частоты wд. Отсюда получаем условие выбора постоянной времени интегрального канала:

С учетом подобного выбора можно оценить значение желаемой ЛАХ на частоте запаса
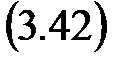
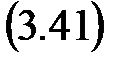
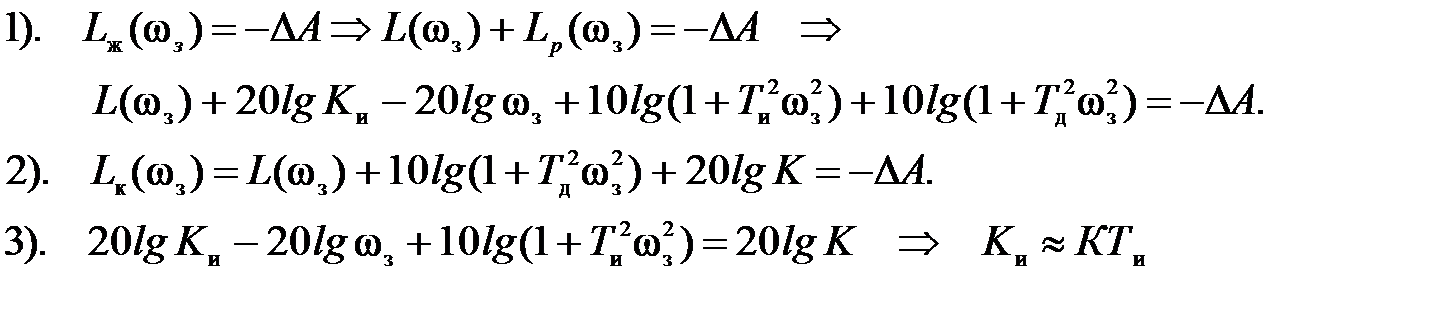
Итак, К и» КТ и, кроме того К п = К и(Т и + Т д), К д = К и Т и Т д, что позволяет вычислить коэффициенты усиления прямого, интегрального и дифференциального каналов ПИД-регулятора.
Если передаточная функция объекта уже обладает нужным порядком астатизма, то интегральный канал регулятора не обязателен, чему соответствует следующий выбор коэффициентов регулятора: К п считаем по описанной выше методике для К и, вычисляем К д = К п Т д (ну а К и = 0 – интегральный канал отсутствует).
7. В результате выполненных расчетов получены все коэффициенты усиления каналов ПИД-регулятора. На заключительной стадии синтеза необходимо провести тестирование частотных и временных свойств замкнутой системы управления:
| -20lg c1 |
| j |
| Lк |
| L |
| Lд |
| wд |
| wи |
| Lж |
| w |
| w |
| L |
| jд |
| jж |
| j |
| wи |
L ж(w) > –DА. Если запас по фазе не обеспечивается, то следует интерактивно подобрать частоты сопряжений wд и wи, не забывая проверять, чтобы амплитуда L ж(wз) не превышала уровня запаса –DА;

Рис. 3.19 – Логарифмические частотные характеристики
желаемой системы
• продолжив низкочастотную асимптоту желаемой логарифмической амплитудно-частотной характеристики L ж(w) до пересечения с осью L, получим отсчет –20 n × lgcn, по которому находим оценку коэффициента ошибки cn. Если оценка не удовлетворяет желаемым требованиям по точности, то можно поднять низкочастотную ветвь амплитудной характеристики путем сдвига вправо частоты сопряжения wи, что равносильно увеличению коэффициента К и и уменьшению постоянной времени Т и при условии постоянства произведения К и Т и;
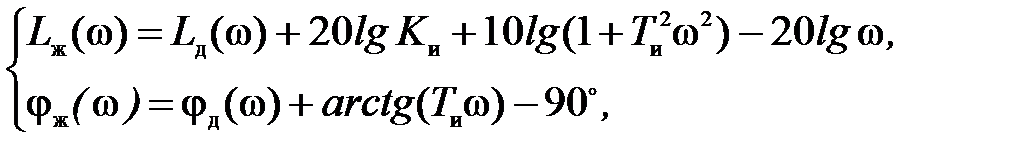
• построив график переходной характеристики замкнутой системы
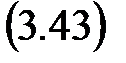
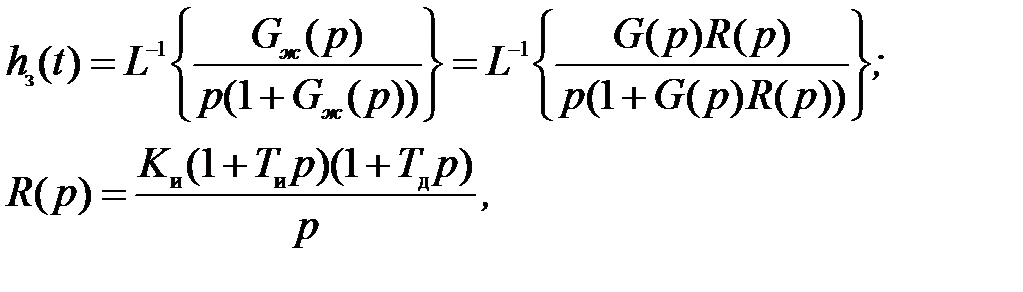
необходимо убедиться в его устойчивости, сходимости к установившемуся значению h з¥ = 1, определить время переходного процесса t пп и перерегулирование s. Полученные показатели переходной характеристики сравниваются с желаемыми значениями и в случае неудовлетворенности разработчика качеством движения интерактивный процесс подбора параметров ПИД-регулятора повторяется.
Пример. Для объекта с передаточной функцией
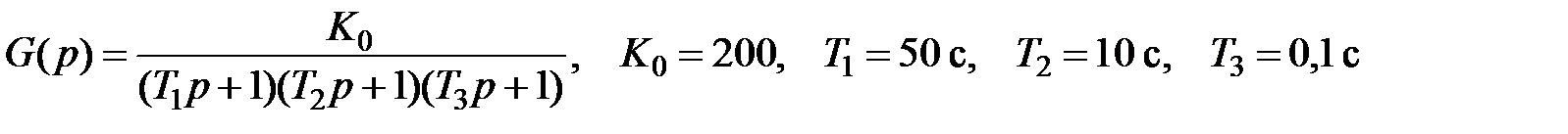
рассчитать ПИД-регулятор, создающий в замкнутой системе астатизм первого порядка с минимальными значениями коэффициента скоростной ошибки с 1, времени переходного процесса t пп и запасами устойчивости по амплитуде D А ³ 6 дБ и фазе Dj ³ p/4.
Следуя изложенному алгоритму, выполняем следующие действия.
1. Строим логарифмические частотные характеристики объекта (рис. 3.20):
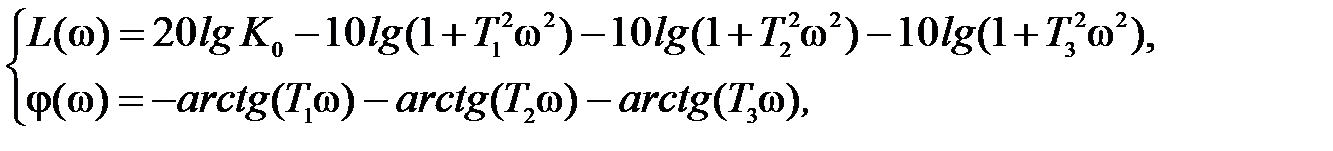
а на осях ординат отмечаем уровни запасов по амплитуде –D А и фазе Dj. Судя по интервалу монотонного уменьшения фазовой характеристики с 0 до –3p/2 и с учетом ее будущего подъема регулятором на высоких частотах на p/2, следует выбрать граничный уровень фазы jгр+Dj = –3p/4.
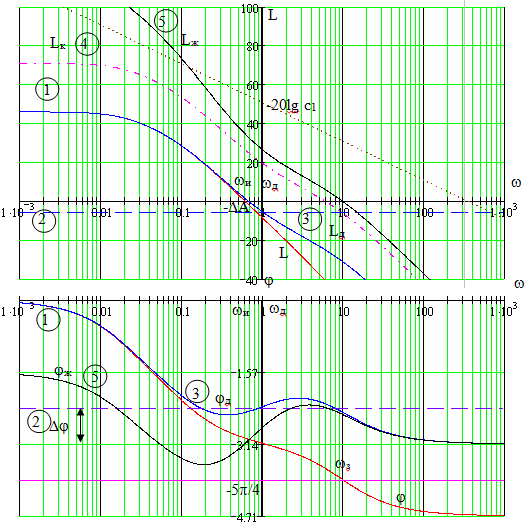
Рис. 3.20. Логарифмические частотные характеристики объекта (1), с дифференциальным звеном (3), с усилителем (4) и желаемой системы (5)
2. Проводим уровень фазы jгр + Dj – p/2 = –5p/4 и по условию
wз: j(wз) = jгр + Dj – p/2
определяем частоту запаса желаемого разомкнутого контура wз = 10 1/с.
3. Выбираем по оценкам wд» 0,1wз, Т д» 10/wз параметры дифференциального канала регулятора: частоту сопряжения wд =1 1/с и постоянную времени Т д =1 с.
4. Строим по формулам
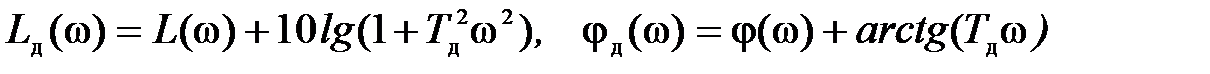
частотные характеристики L д(w) и jд(w) последовательного соединения объекта G (p) с форсирующим звеном регулятора
1+ Т д р = p +1.
5. Определяем отклонение амплитуды L д(wз) от уровня запаса –DА:  и по формуле
и по формуле 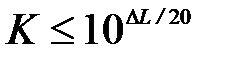 вычисляем коэффициент К: D L = 25 дБ Þ К = 17,8.
вычисляем коэффициент К: D L = 25 дБ Þ К = 17,8.
6. С учетом фазового сдвига от –p/2 до 0, вносимого изодромным звеном в диапазоне частот w £ 10 wи, из условия  с небольшим запасом выбираем параметры интегрального канала регулятора: частоту сопряжения wи = 0,5 1/с и постоянную времени Т и = 2 с. Тогда по соотношениям К и» КТ и,
с небольшим запасом выбираем параметры интегрального канала регулятора: частоту сопряжения wи = 0,5 1/с и постоянную времени Т и = 2 с. Тогда по соотношениям К и» КТ и, 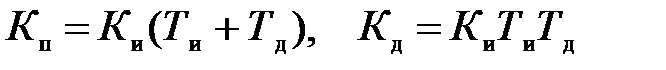 получаем коэффициенты усиления прямого, интегрального и дифференциального каналов ПИД-регулятора:
получаем коэффициенты усиления прямого, интегрального и дифференциального каналов ПИД-регулятора:
К и = 8,8; К п = 26,4; К д = 17,6.
7. В результате проведенных графических расчетов получена передаточная функция ПИД-регулятора:

Построив частотные характеристики желаемой разомкнутой системы

убеждаемся в наличии желаемых запасов устойчивости D А и Dj.
Продолжение низкочастотной части характеристики L ж(w) отсекает на оси ординат при w = 1 значение –20 lgc 1» 64 дБ (c 1 = 1/ К), из чего заключаем, что коэффициент скоростной ошибки составляет c 1 < 0,001 с.
Сформировав передаточную функцию желаемой разомкнутой системы
G ж(p) = G (p)∙ R (p),
построим переходную характеристику замкнутой системы (рис. 3.21) и определим ее показатели качества t пп = 1,05 с и s = 31,1 %.
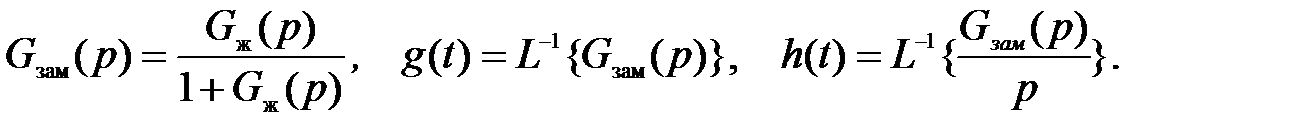
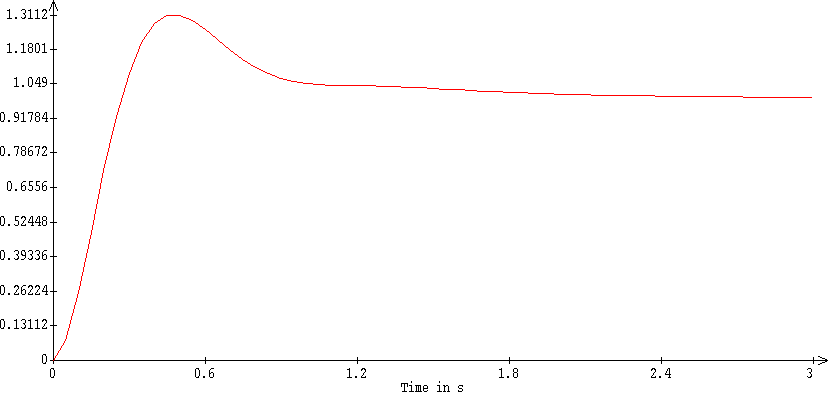
Рис. 3.21. Переходная характеристика желаемой системы
В современных цифровых системах управления вместо непрерывного ПИД-управления, вырабатываемого аналоговой схемой, реализуется алгоритм вычисления управляющих воздействий xk = x (tk) в дискретные отсчеты времени tk с помощью микропроцессорного контроллера. В первом приближении, т. е. без попыток какой-либо оптимизации численного интегрирования и дифференцирования, закон дискретного управления записывается в следующем виде


Поиск по сайту: