Критерий устойчивости Гурвица 3 страница

Входным напряжением u_ВХюОУ ОУ является разность потенциалов прямого и инверсного входов:

u_ВХ.ОУ = φ_П – φ_И

Коэффициент усиления ОУ очень велик

Из-за большого коэффициента усиления К_ОУ выходное напряжение u_ВЫХ достигает значения насыщения (около | Е-1 | В) при малом значении входного напряжения . При таком малом значении u_ВХ допустимо в расчетах принимать u_ВХ.ОУ ≈0, что существенно упрощает расчеты схем на базе ОУ.

Основная схема включения ОУ приведена на рис.1.58. Прямой вход ОУ заземлен через резистор R_TK, поэтому потенциал прямого входа φ_П нулевой. В активном режиме работы ОУ, когда выходное напряжение u_ВЫХ изменяется прямо пропорционально входному напряжению u_ВХ схемы, входное напряжение ОУ u_ВХ.ОУ ≈0 и, поэтому, потенциалы обоих входов ОУ равны между собой: φ_И =φ_П. Так как φ_П=0, то будет также φ_И=0.

Рассчитаем по формуле метода двух узлов потенциал φ_И инверсного входа:

(1.63)

После подстановки φ_И=0 в (1.63) получим

где передаточная функция схемы:

(1.64)

Резистор температурной компенсации R_TK служит для обеспечения температурной стабильности схемы. Сопротивление резистора выбирается из условия равенства активных проводимостей цепей протекания постоянного по прямому и инверсному входам

(1.65)

Схема П-регулятора приведена на рис.1.59. Расчеты П-регулятора:

Схема И-регулятора приведена на рис.1.60. Расчеты И-регулятора:

Схема ПИ-регулятора приведена на рис.1.61. Расчеты ПИ-регулятора:

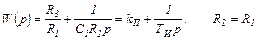
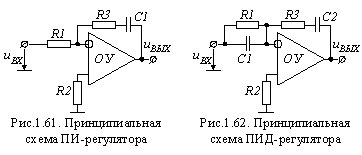
Схема ПИД-регулятора приведена на рис.1.62. Расчеты ПИД-регулятора:

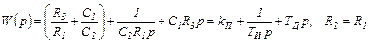
Расчеты регуляторов, реализованных на базе операционных усилителей, действительно являются простыми и основаны на использовании всего двух формул - (18.5) и (18.6).

Вопросы и задания

1. Перечислите основные характеристики и эксплуатационные достоинства операционных усилителей.

2. Какова основная схема включения ОУ? Приведите вывод передаточной функции основной схемы включения ОУ.

3. Приведите принципиальные электрические схемы П- и И-регуляторов и расчет элементов схем.

4. Приведите принципиальные электрические схемы ПИ- и ПИД- регуляторов и расчет элементов схем.

5. Рассчитать, задавшись коэффициентами передачи и постоянными времени регулятора (по выбору преподавателя) сопротивления резисторов и емкости конденсаторов схемы регулятора.

1.18. Схемы корректирующих устройств

на пассивных элементах

Корректирующим устройством (КУ) называется звено САУ, используемое в качестве регулятора, если его передаточная функция не приводится ни к одной передаточной функции типового регулятора П-, И- и Д-типов. В связи с этим, схем корректирующих устройств и их типов существуют бесконечно много. Ниже рассмотрено две наиболее применимые на практике схемы КУ.

Интегро-дифференцирующее корректирующее устройство

Передаточная функция интегро-дифференци-рующего корректирующего устройства имеет вид

,

где k - коэффициент передачи КУ;

τ и Т – постоянные времен КУ, причем τ<T.

Схема на резисторах и конденсаторе приведена на рис.1.63. Рассчитаем схему:

откуда

где (1.66)

Числовой пример.

Рассчитать элементы схемы интегро-дифференцирующего КУ, если

Решение.

Составляем, используя (1.66), систему уравнений

(1.67)

Система (1.67), состоящая из двух уравнений с тремя неизвестными, неразрешима. Необходимо задать характеристику одного из элементов, а другие характеристики рассчитать.

Задаём ёмкость конденсатора С₁=1 мкФ. Тогда из (1.67) найдём

Дифференциально-интегрирующее корректирующее устройство

Передаточная функция дифференциально-интегрирующего корректирующего устройства имеет вид

,

где k - коэффициент передачи КУ;

τ и Т – постоянные времен КУ, причем τ<T.

Схема на резисторах и конденсаторе приведена на рис.1.64. Рассчитаем схему:

откуда

где (1.68)

Числовой пример.

Рассчитать элементы схемы дифференциально-интегрирующего КУ, если

Решение.

Составляем, используя (19.6), систему уравнений для постоянных времени:

(1.69)

Задаемся ёмкостью конденсатора С₁=1 мкФ. Из (1.69) найдём

,

а из (1.68)

Вопросы и задания

1. Приведите схему интегро-дифференцирующего КУ и выполните для нее вывод передаточной функции.

2. Приведите пример числового расчета интегро-дифференцирующего КУ с выбором стандартных элементов схемы.

3. Приведите схему дифференциально-интегрирующего КУ и выполните для нее вывод передаточной функции.

4. Приведите пример числового расчета дифференциально-интегрирующего КУ с выбором стандартных элементов схемы.

1.19. Схемы корректирующих устройств

на активных элементах

КУ на пассивных элементах имеют следующие недостатки:

1. Коэффициент передачи КУ не превышает единицы, и, поэтому, требуется вводить в КУ пропорциональными усилителями.

2. Последовательное включение пассивных КУ недопустимо из-за взаимного влияния их, что приводит к искажению передаточных функций отдельных КУ. Так, если два последовательно включенных КУ имеют передаточные функции W₁ (p) и W₂ (p), то эквивалентная передаточная функция не равна произведению передаточных функций отдельных КУ:

W_ЭКВ (p) ≠ W₁ (p) ·W₂ (p)

3. Для согласования цепи последовательно включенных КУ между ними необходимо устанавливать согласующие усилители, которые имеют большое входное и малое выходное сопротивления.

Схемы КУ на активных элементах свободны от этих недостатков за счет того, что в их состав входят ОУ.

Полное КУ содержит во входной цепи и в цепи обратной связи ОУ схемы из резисторов и конденсаторов. Если в цепи обратной связи используются только резисторы, то ОУ отводится роли усилителя сигнала и согласующего звена.

КУ с активно-емкостными элементами на входе и в цепи обратной связи приведено на рис.1.65. Передаточная функция данного КУ согласно (1.64) имеет вид

За счет выбора значений сопротивлений резисторов R1 и R2 и емкостей конденсаторов С1 и С2 можно получить любое значение коэффициента передачи k и любое соотношение Т₁ / Т₂. постоянных времениКУ. которое может быть звеном как интегро-дифференцирующим, так и дифференциально-интегрирующим.

Схема КУ, в которой усилитель на базе ОУ выполняет роль согласующего элемента, приведена на рис.1.66. ОУ включен между двумя пассивными КУ.

Усилитель на ОУ своим сопротивлением R1 шунтирует пассивное КУ1. Чтобы такое шунтирование не изменило передаточной функции КУ1, необходимо, чтобы выполнялось соотношение

, (1.69)

где 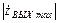- максимальное значение модуля выходного сопротивления КУ1, которое равно выходному сопротивлению схемы, в которой все конденсаторы представлены в виде обрывов цепи.

Например, для схемы на рис.1.63 , а для схемы на рис.1.64 .

Пассивное КУ2 является нагрузкой ОУ. Минимальное значение входного сопротивления КУ2, которое равно входному сопротивлению схемы, в которой все конденсаторы представлены в виде перемычек. Например, для схемы на рис.1.63 , а для схемы на рис.1.64 .

Сопротивление должно выбираться из условий:

- недопущения перегрузки по току

; (1.70)

- ограничения на сопротивление нагрузки ОУ

(1.71)

Значение выбирается большим из двух значений, определенных по (1.70) и (1.71).

При выполнении условий (1.69)…(1.71) эквивалентная передаточная схемы

W_ЭКВ(p)= k_ОУ·W_КУ1(p)·W_КУ2(p),

где – коэффициент усиления схемы на ОУ, который по условиям устойчивости схемы не должен быть более 100.

Вопросы и задания

1. Приведите схему полного КУ на базе ОУ и выполните вывод его передаточной функции.

2. Приведите схему КУ с согласующим элементом на базе ОУ. В чем состоит смысл согласования?

3. Приведите оценки входных и выходных сопротивлений пассивных КУ, рассмотренных в теме 1.18.

1.20. Коррекция линейных САУ

с помощью местных обратных связей

Для того, чтобы изменить характеристики отдельных звеньев САУ и этим обеспечить устойчивость и заданные показатели качества замкнутой САУ, целесообразно применять местные обратные связи.

Варианты исполнения местных обратных связей отражены на рис.1.67.

Варианты коррекции:

1. Превращение интегрирующего звена, которое в динамическом отношении является звеном, находящимся на грани устойчивости, в инерционное звено 1-го порядка. Для этого надо применить ЖООС (рис.1.68). Передаточная функция схемы

2. Уменьшение постоянной времени инерционного звена 1-го порядка, достигаемое с помощью ЖООС (рис.1.69), уменьшает также коэффициент передачи звена:

Недостатком данной коррекции является то, что вместе с уменьшением постоянной времени инерционного звена в 1+К·К_ОС раз во столько же раз уменьшается коэффициент передачи. Применение ГПОС позволяет избежать этого недостатка (рис.1.70):

3. Превращение колебательного звена в апериодическое звено 2-го порядка достигается применением ЖПОС (рис.1.71).

У исходного колебательного звена дискриминант отрицательный .

При введении жесткой положительной обратной связи передаточная функция схемы примет вид:

Дискриминант для характеристического многочлена эквивалентной передаточной функции выбором значения К_ОС может быть сделан положительным, что является признаком действительных корней характеристического уравнения и, соответственно, апериодического звена 2-го порядка. Одновременно с этим уменьшается коэффициент передачи звена в (1-К·К_ОС ) раз. Устранить этот недостаток можно применением гибкой обратной связью вместо жесткой.

4. Превращение звена с любой передаточной функции W(p) в звено с любой наперед заданной передаточной функцией W_ЭКВ(p) производится по рис.21.6.

Эквивалентная передаточная функция схемы

(1.72)

Если в диапазоне существенных частот (частот, которые являются основными в сигналах САУ) коэффициент передачи разомкнутой САУ, равный произведению коэффициентов передачи звена и цепи обратной связи К_ЗВК_ОС является очень большим числом, то будет справедливо выражение

1+W_OC (р) W_ЗВ (р) ≈ W_OC (р) W_ЗВ (р)

Передаточная функция (1.72) превратится в

(1.73)

Этот результат показывает, что вид эквивалентной передаточной функции W_ЭКВ (р) определяется только передаточной функцией W_OC (р) цепи обратной связи и совсем не зависит от передаточной функции W_ЗВ (р) исходного звена.

В качестве примера рассмотрим реализацию ПД-регулятора. Если в качестве исходного звена использовать пропорциональное звено с большим коэффициентом усиления К_ЗВ, а в цепи обратной связи использовать инерционное звено первого порядка , то эквивалентная передаточная функция будет иметь вид

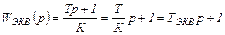
Полученный таким способом ПД-регулятор содержит идеальное Д-звено и, как показывает опыт, достаточно устойчив к помехам.

Вопросы и задания

1. Какие виды обратной связи применяют для коррекции линейных САУ?

2. Как превратить интегрирующее звено, в динамическом отношении находящемся на грани устойчивости, в устойчивое апериодическое звено?

3. Как уменьшить постоянную времени апериодического звена?

4. Как превратить колебательное звено в апериодическое звено 2-го порядка?

5. Как превратить звено с произвольной передаточной функцией в звено с наперед заданной передаточной функцией?

6. Как можно получить помехоустойчивый ПД-регулятор?

1.21. Пример судовой линейной САУ

Рассмотрим САУ курсом судна, в которую входят неизменяемая часть Н и авторулевой АР (рис.1.73а). Авторулевой представляет собой ПИД-регулятор

(рис. 1.73б). Неизменяемая часть содержит (рис. 1.73в): исполнительный двигатель ИД, рулевую машинку РМ и судно С как объект управления. ИД и РМ вместе образуют рулевой привод РП судна.

На схеме обозначены:

- заданный х и фактический у курсы судна и сигнал ε ошибки курса;

- перемещение h штока золотника гидравлической рулевой машинки и угол β поворота руля.

Неизменяемая часть САУ имеет астатизм 3-го порядка (см. тему 1.13) и при охвате ее единичной обратной связью образуется неустойчивая замкнутая САУ. Для понижения порядка астатизма неизменяемой части применим местные жесткие отрицательные обратные связи (см. тему 1.21) с очень большими коэффициентами передачи, охватив ими исполнительный двигатель ИД с рулевой машинкой РМ по схеме, приведенной на рис.1.74. Эквивалентная передаточная функция W₁ (p) охваченного жесткой ООС исполнительного двигателя ИД с К_ОС1→∞ имеет согласно (1.73) вид

Повторная обратная связь при К_ОС2→∞ на рис.1.74 превращает рулевой привод РП в эквивалентное пропорциональное звено

Структурная схема САУ примет вид, приведенный на рис.1.75.

Настраиваемыми параметрами авторулевого являются коэффициент передачи k_П пропорциональной части и постоянная времени Т_Д дифференциальной части. В зависимости от условий плавания (ветер, волны, глубина фарватера), загрузки судна (порожнее или груженное) изменяются его параметры k_С и Т_С.

Используя критерий устойчивости Гурвица, определим значения k_П и Т_Д параметров настройки авторулевого из условия обеспечения устойчивости САУ. Для этого найдем передаточную функцию замкнутой САУ

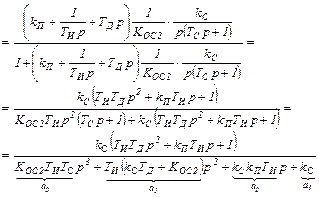
Определитель Гурвица и условия устойчивости

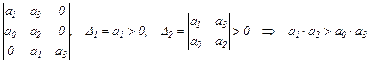
или

(1.74)

Границей, разделяющей области устойчивости и неустойчивости, является линия (рис.1.76), описываемая в осях k_П и Т_Д уравнением

, (1.75)

которое получено из последнего неравенства (1.74) путем замены знака неравенства на знак равенства.

Подставим в неравенство (1.74) значения k_П=0 и Т_И=0. Неравенство не будет выполняться. Значит ниже линии (1.75) будет область неустойчивости, а выше – устойчивости.

Положение линии границы устойчивости зависит от параметров k_С и Т_С судна, что следует из выражения (1.75). Чтобы САУ судна была устойчивой при любых значениях k_С и Т_С, необходимо построить множество границ устойчивости и соответствующих им частных областей устойчивости. Область, общая для всех частных областей, является областью устойчивости САУ в любых условиях эксплуатации судна.

Передаточная функция разомкнутой САУ курсом судна W_РАЗ (p), получаемая в результате перемножения передаточных функций авторулевого W_АР (p), рулевого привода W_РП.ЭКВ (p) и судна W_С (p), будет иметь сомножителем р² в знаменателе. Значит САУ будет астатической 2-го порядка и, поэтому, как статическая ε_СТ, так и скоростная ε_СК ошибки регулирования будут нулевыми (см. тему 1.12).

Вопросы и задания

1. Какие элементы входят в САУ курсом судна и какие их передаточные функции?

2. Зачем элементы рулевого привода дважды охвачены жесткими обратными связями?

3. Как исследовать на устойчивость САУ курсом судна?

4. Как обеспечить устойчивость САУ курсом судна в любых условиях его эксплуатации? Каковы ошибки удержания судна на заданном курсе?

1.22. Сущность процесса синтеза САУ.

Частотный метод синтеза линейных САУ

Синтез САУ представляет собой процедуры определения вида и характеристик корректирующего устройства или регулятора, с помощью которых система с исходным набором звеньев и их характеристик при заданных внешних задающих и возмущающих воздействиях работает с заданным качеством.

Методы синтеза классифицируются по критериям (показателям качества), используемых при синтезе, характеристиками входных сигналов, структурой исходной схемы и алгоритм решения задачи синтеза.

Синтез КУ следящих систем производится частотным методом с использованием ЛАЧХ по обобщенной структурной схеме САУ, приведенной на рис.1.77.

Исходные данные для синтеза:

1. Передаточная функция W_Н (p) неизменяемой части САУ.

2. Показателями качества (критериями синтеза) являются:

- максимальная ошибка регулирования ε_т в следящем режиме;

- показатель колебательности М.

Ошибка регулирования ε_т является прямым показателем качества, а показатель колебательности М – косвенным. Зная М, можно по рис.1.47 найти перерегулирование σ.

3. Характеристиками входного сигнала являются: максимальные скорость и ускорение 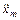его изменения.

Этапы синтеза:

1. Строится ЛАЧХ неизменяемой части системы L_Н, например, вида, изображенного на рис.1.78.

2. Строится желаемая ЛАЧХ L_Ж синтезированной САУ (рис.23.2). Желаемая ЛАЧХ L_Ж состоит из четырех участков: низкочастотного (НЧ), среднечастотного (СЧ), высокочастотного (ВЧ) и сверхвысокочастотного (СВЧ).

Построение НЧ участка. Форма L_Ж на НЧ участке определяется требованием точности ε_т с учетом параметров и 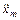входного сигнала. Участок состоит из двух отрезков, исходящих из контрольной точки К с координатами ω_К и L_K, с наклонами –1 и –2. Сначала определяется базовая частота

.)

Затем рассчитываются координаты контрольной точки К:

Ниже отмеченных прямых находится запретная область. Если L_H проходит через запретную область, то заданная точность ε_т в следящем режиме не будет обеспечена и, поэтому, необходимо вводить корректирующее устройство КУ.

Построение СЧ участка. Форма L_Ж на CЧ участке определяется требованием обеспечения заданного показателя колебательности М с учетом параметров и 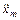входного сигнала. СЧ участок состоит из одного отрезка с наклоном –1. Границы отрезка по оси частот определяются двумя частотами сопряжения w_t и 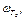которые определяются через постоянные времени

В диапазоне частот СЧ участка проверяется то, чтобы резонансный выброс ЛАЧХ L_Нd не заходил в запретную область.

Построение ВЧ участка. ВЧ участок влияет только на показатель колебательности М, располагается в диапазоне частот от до граничной w_ГР, равной w_ГР»40w₀, и должен состоять из одного отрезка с наклоном -2. Однако с целью получения наиболее простой схемы корректирующего устройства КУ допускается введение на ВЧ участке дополнительных изломов с последующим пересчетом частоты . Упрощение схемы КУ достигается при условии, что в диапазоне частот от до w_ГР желаемая ЛАЧХ L_Ж будет повторять все изломы ЛАЧХ L_Нd. В нашем примере нужно повторить излом на частоте w₂ с одновременным пересчетом постоянной времени и частоты сопряжения правого конца СЧ участка:

Построение СВЧ участка. СВЧ участок располагается правее частоты w_ГР. Он не влияет ни на один показатель качества и его форма определяется только требованиями получения наиболее простой схемы корректирующего устройства КУ. Упрощение схемы КУ достигается при условии, что желаемая ЛАЧХ L_Ж будет повторять все наклоны ЛАЧХ L_Н.

3. По ЛАЧХ L_Ж восстанавливается желаемая передаточная функция САУ. Так для приведенной на рис.23.2 ЛАЧХ L_Ж передаточная функция будет

При известной передаточной функции W_H (р) неизменяемой части передаточная функция КУ находится из выражения

Вопросы и задания

1. Сформулируйте постановку задачи и исходные данные для синтеза следящей САУ.

2. Какие исходные данные определяют форму НЧ участка желаемой ЛАЧХ? Что такое "запретная область"?

3. Какие исходные данные определяют форму СЧ участка желаемой ЛАЧХ?

4. Как строятся ВЧ и СВЧ участки желаемой ЛАЧ?

2. САУ СО СЛУЧАЙНЫМИ СИГНАЛАМИ

Поиск по сайту: