 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Не градиентные методы
Не градиентные методы применяются для организации рабочих шагов в САУ, когда количество управляющих сигналов и1, и2, …, ип слишком велико (несколько десятков), когда целевая функция имеет несколько экстремумов (рис.6.6б) и также в случаях, когда требование простоты блока адаптации (БА на рис.6.2) является решающим фактором.
Метод покоординатной оптимизации (метод Гаусса-Зайделя)
Этот метод наиболее часто применяется в системах, где для многопараметрической оптимизации (поиска экстремума для объектов с несколькими управляющими входами) используются простые одноканальные экстремальные регуляторы, позволяющие находить экстремум функции одного переменного. При таком методе поиска изменяется один из управляющих параметров (при всех остальных зафиксированных и, поэтому, неизменных) до тех пор, пока не будет достигнут экстремум по этому параметру. После этого начинается аналогичный поиск экстремума по другой переменной при всех остальных зафиксированных.
Траектория поиска по методу Гаусса-Зайделя показана на рис.6.7 (9-10-11-12-13). Как видно, вначале изменяется и2 при и1=const до точки касания линии движения с линией уровня (точка 10), где выполняется условие dJ/du2=0. Затем аналогично изменяется переменная и1 и т. д.
Метод случайного поиска (метод Монте Карло)
Если целевая функция имеет несколько экстремумов (рис.6.6б) и нет абсолютно никакой информации о расположении экстремальных точек в области управляющих сигналов и1, и2, …, ип, то эффективным может быть метод случайного поиска. Суть метода в том, что задаются случайные значения управляющим сигналам и1, и2, …, ип и этим на ощупь определяются области возможных экстремумов. Естественно, затраты времени на осуществление случайного поиска будут большими.
Когда области возможных экстремумов установлены, то на заключительном этапе можно перейти к градиентным методам или к методу Гаусса-Зайделя.
Если в процессе работы САУ может измениться карта целевой функции, то нужно эпизодически возвращаться к чистому случайному поиску.
Метод сканирования (полного перебора)
Если целевая функция имеет несколько экстремумов и о расположении экстремальных точек в области управляющих сигналов и1, и2, …, ип, нет никакой информации, то наряду со случайным поиском может оказаться эффективным перебор значений всех управляющих сигналов – метод сканирования. Теоретически такой перебор потребует неограниченного времени. Для сокращения времени выхода на точку глобального экстремума нужно методом проб и ошибок наращивать величины изменений Δи1, Δи2, …, Δип управляющих сигналов и сочетать полный перебор со случайным выбором начальной точки движения.
Симплекс-метод (метод триангуляции)
Этот является улучшенных вариантом метода покоординатной оптимизации.
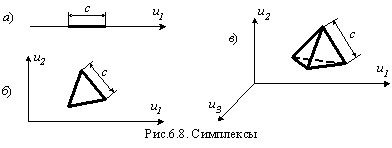
Симплексом называют простейшие фигуры в соответствующих пространствах. На рис.6.8 показаны симплексы: одномерный — отрезок прямой (рис.6.8а), двумерный - треугольник (рис.6.8б), трехмерный—четырехгранная пирамида (рис.6.8в).
 Идея симплекс-метода поясняется на примере двумерной задачи (рис.6.9). Как и раньше, оптимизируемая функция, имеющая максимум, изображается на плоскости с помощью линий уровня. В исходной области в трех точках (1, 2, 3), являющихся вершинами симплекса, определяются соответственно значения целевой функции: J1, J2 и J3. Эти значения упорядочиваются по величине, например, пусть получено
Идея симплекс-метода поясняется на примере двумерной задачи (рис.6.9). Как и раньше, оптимизируемая функция, имеющая максимум, изображается на плоскости с помощью линий уровня. В исходной области в трех точках (1, 2, 3), являющихся вершинами симплекса, определяются соответственно значения целевой функции: J1, J2 и J3. Эти значения упорядочиваются по величине, например, пусть получено  . Следующая точка 4 находится как зеркальное отображение вершины симплекса с наименьшим значением функции J1 относительно стороны, опирающейся на точки со значениями J2 и J3. Образуется новый симплекс J2, J3 и J4. Вычисляется значение целевой функции J4 в точке 4 образовавшегося симплекса (2, 3, 4). Пусть для него получено соотношение
. Следующая точка 4 находится как зеркальное отображение вершины симплекса с наименьшим значением функции J1 относительно стороны, опирающейся на точки со значениями J2 и J3. Образуется новый симплекс J2, J3 и J4. Вычисляется значение целевой функции J4 в точке 4 образовавшегося симплекса (2, 3, 4). Пусть для него получено соотношение  . Следующая точка 5 находится как зеркальное отображение вершины J2 относительно стороны, опирающейся на точки J3 и J4. Подобным образом осуществляется шаг за шагом движение к экстремальной точке по траектории (5-6-7-8-9-10-11-12).
. Следующая точка 5 находится как зеркальное отображение вершины J2 относительно стороны, опирающейся на точки J3 и J4. Подобным образом осуществляется шаг за шагом движение к экстремальной точке по траектории (5-6-7-8-9-10-11-12).
Как показывают числовые эксперименты, симплекс-метод по времени поиска экстремума эффективнее метода покоординатной оптимизации, так как, по существу, позволяет совершать движение одновременно по всем сигнала управления и1, и2, …, ип. Кроме того, симплекс-метод позволяет находить локальные экстремумы, для чего нужно периодически случайным образом задавать три начальных точки в плоскости сигналов управления. Возможен также симплекс-метод с изменяющейся длиной стороны симплекса, а именно, в начале движения нужно задавать большое значение с длины стороны симплекса, а по мере приближения к экстремуму длину с стороны нужно уменьшать.
Симплекс-метод позволяет решать задачи оптимизации в самых сложных ситуациях, когда количественная оценка оптимизируемой функции затруднена и удается получать лишь качественные суждения типа: "в этой точке значение J – наихудшее", так как для дальнейшего движения важно указать лишь одну наихудшую точку.
Вопросы и задания
1. Какие методы движения к экстремуму применяются в экстремальных САУ? Что нужно учитывать при выборе такого метода?
2. Поясните градиентные методы.
3. Поясните методы покоординатной оптимизации, случайного поиска и сканирования.
4. Поясните симплекс-метод.
6.4. Пример экстремальной САУ асинхронного
электропривода по минимуму потребляемого тока
Электродвигатель как элемент электропривода должен обеспечить заданные значения момента М и частоты вращения ω (рис.6.10). Если требуется регулирование частоты вращения, то для питания АД целесообразно использовать в качестве источника питания преобразователь частоты (ПЧ) с раздельным регулированием величины U и частоты f напряжения статора АД. Частота вращения ω практически целиком определяется частотой f напряжения статора АД. Если частота вращения ω АД, однажды установленная, не меняется, то это значит, что частота f питающего напряжения зафиксирована.
 От источника питания АД потребляет ток IS. Величина тока IS зависит от величин U и f напряжения статора и величины момента сопротивления МС нагрузки. Качественно эти зависимости выглядят следующим образом:
От источника питания АД потребляет ток IS. Величина тока IS зависит от величин U и f напряжения статора и величины момента сопротивления МС нагрузки. Качественно эти зависимости выглядят следующим образом:
1. При изменениях момента сопротивления нагрузки МС пропорционально ему изменяется ток статора IS;
2. При значительном понижении величины U напряжения статора и зафиксированной частоте f двигатель, чтобы развить вращающий момент равный моменту сопротивления МС нагрузки, ток статора должен возрасти, так как
 ~
~ 
где ωД – частота вращения вала АД, которая прямо пропорциональна частоте f питающего напряжения;
η и cosφ – к.п.д. и коэффициент мощности АД.
3. При значительном повышении величины U напряжения статора и фиксированной частоте f магнитопровод статора входит в насыщение, поэтому резко уменьшается индуктивное сопротивление АД по цепи основного магнитного потока и ток статора возрастает. Объяснением этому являются следующие три положения:
- амплитуда Фт магнитного потока статора прямо пропорциональна напряжению U, приложенному к катушкам статора,
U~4,44·f·w·Фт;
- напряженность Н магнитного поля статора прямо пропорциональна току IS в его обмотках;
- связь между напряженностью Н и магнитным потоком Фт нелинейная и, следовательно, нелинейна связь между током IS и напряжением U, причем ток IS растет быстрее напряжения U, например, при увеличении напряжения U на 20% ток IS возрастает в 2…3 раза (рис.6.11).

Таким образом, на качественном уровне установлено возрастание тока статора АД как при чрезмерном уменьшении, так и при чрезмерном увеличении напряжения статора, если частота питающего напряжения постоянна. Отсюда следует, что должно существовать такое напряжение U питания статора, при котором ток статора IS минимален.
Такие зависимости представлены на рис.6.12 для малой МН и большой БН механической нагрузок.

Рассмотрим работу адаптивного асинхронного электропривода, приняв качестве управляемого сигнала напряжение U статора АД, а в качестве целевой функции – ток статора IS, который нужно минимизировать.
Примем большую первоначальную загрузку АД и режим его электропотребления, обозначенный точкой 0 на графике БН с током I0. Далее блок адаптации выполняет совмещено пробные и рабочие шаги:
1). Напряжение U уменьшается на величину ΔU. По истечении времени переходного процесса в обмотках статора АД его ток примет значение I1, соответствующее точке 1. Вычисляется разность токов ΔI10=I1-I0 . Так как изменение тока положительное (ΔI10>0), то шаг 0-1 сделан в неверном направлении.
2). Напряжение U увеличивается на величину ΔU. По истечении времени переходного процесса в обмотках статора АД его ток примет значение I0, соответствующее точке 0.
3). Напряжение U увеличивается на величину ΔU. По истечении времени переходного процесса в обмотках статора АД его ток примет значение I2, соответствующее точке 2. Вычисляется разность токов ΔI20=I2-I0. Так как изменение тока отрицательное (ΔI20<0), то шаг 0-2 сделан в верном направлении..
4). Напряжение U увеличивается на величину ΔU. По истечении времени переходного процесса в обмотках статора АД его ток примет значение I3, соответствующее точке 3. Вычисляется разность токов ΔI32=I3-I2 . Так как изменение тока положительное (ΔI32>0), то шаг 2-3 сделан в неверном направлении.
5). Снова возврат на точку 2 и определение тока I2.
6). Шаг в точку 0 и повторение уже вышеописанных шагов.
САУ будет совершать автоколебания за счет повторяющихся проходов точек по цепи 0-2-3-2-0-2-3-…. Ток статора будет удерживаться на минимальном уровне в окрестности точки 2.
Пусть в тот момент, когда напряжение статора было равным U0, соответствовало точке 0 на графике БН, нагрузка АД уменьшилась, так что график IS (U) принял форму графика МН (рис.6.11). Измеренный при этом ток стал равным I4. Так как изменение тока ΔI24=I2-I4, то этот шаг воспримется блоком адаптации как правильный. Поэтому следующий шаг будет сопровождаться уменьшением напряжения U с выходом на точку 6. Далее блок адаптации, двигаясь по графику МН, выйдет в окрестность точки 7. Автоколебания установятся по цепи точек 7-8-7-6-7-…. Ток статора будет удерживаться на минимальном уровне в окрестности точки 7.
Для уменьшения амплитуда автоколебаний необходимо уменьшать шаг ΔU, а для ускорения выхода на минимум тока – нужно ΔU увеличивать. Таким образом очевидна целесообразность изменения шага ΔU в зависимости от близости к точке минимума тока. В качестве критерия изменения величины шага ΔU можно принять величину ΔI изменения тока статора на очередном шаге. При уменьшении ΔI, что свидетельствует о приближении к точке минимума графика, нужно также уменьшать шаг ΔU.
Вопросы и задания
1. Обоснуйте экстремальный вид графика зависимости тока статора АД от напряжения его питания.
2. Поясните работу блока адаптации при управлении напряжением питания АД при постоянной его механической нагрузке.
3. Поясните работу блока адаптации при управлении напряжением питания АД при изменении его механической нагрузки.
4. Как можно ускорить работу и повысить точность в рассмотренной экстремальной САУ?
6.5. Структура и принцип действия
беспоисковых адаптивных САУ
Беспоисковые адаптивные САУ имеют обобщенную структурную схему одного из двух видов:
- с эталонной моделью объекта управления или всей классической (не адаптивной) САУ;
- с восстановленной наблюдающим устройством моделью объекта управления.
На рис.6.13 приведена обобщенная структурная схема адаптивной САУ с эталонной моделью исходной замкнутой САУ, которая состоит из объекта управления ОУ и линейного регулятора. Регулятор может быть любого типа, но на рис.6.13, для определенности изложения, приведен ПИД-регулятор. Также вместо эталонной модели замкнутой САУ может быть использована эталонная модель объекта управления, для чего на вход эталонного звена с передаточной функцией WЭ (р) нужно подать тот же сигнал, который поступает на вход объекта управления с передаточной функцией WОУ (р).
В приведенной адаптивной САУ сравниваются действительный у сигнал, выходящий с исходной замкнутой САУ, и эталонный уЭ, формируемый эталонным звеном. Сигнал ошибки Δу=уЭ-у поступает на блок адаптивного управления БАУ. При несовпадении сигналов у и уЭ (Δу≠0) БАУ вырабатывает корректирующие сигналы, которые заводятся в исходную САУ так, чтобы было минимизировано расхождение сигналов у и уЭ (в идеале должно быть достигнуто Δу=0). Коррекция может быть сигнальной или параметрической.

При сигнальной коррекции БАУ вырабатывает сигнал Δи, который поступает в виде дополнительного сигнала либо на вход регулятора (замкнут ключ S1), либо на вход объекта управления (замкнут ключ S3). Этот вид коррекции достаточно хорошо проработан теоретически. В качестве эталонного звена может быть принято звено, передаточная функция WЭ(р) которого:
1) По структуре совпадает с передаточной функцией объекта управления WОУ (р). В этом случае БАУ может быть простейшего вида (см. рис.6.14 и 6.15).
2). По структуре может быть любого желаемого вида, например пониженного в сравнении с WОУ (р) порядка и простейшего вида – пропорциональное звено, апериодическое звено 1-го порядка и т.п. В таком случае БАУ реализует скользящий режим работы адаптивной САУ. Работа БАУ имеет сложный характер, однако эта сложность непринципиальна, так как вопрос организации скользящего режима полностью решен теоретически.
При параметрической коррекции БАУ вырабатывает сигналы ΔkП, ΔТИ и ΔТД, которыми корректируются параметры kП, ТИ и ТД настройки регулятора (замкнут ключ S2). Этот вид коррекции не имеет исчерпывающего теоретического обоснования в рамках классических способов управления, т.е. не существует процедур и алгоритма, позволяющих обоснованно производить перестройку значений kП, ТИ и ТД. Однако эта же задача имеет процедуры в классе интеллектуальных технологий управления, таких как нечеткие регуляторы (фаззи-регуляторы). Эти виды управления основаны на использовании опыта человека по управлению сложными системами, когда используются неформализованные (не подтвержденные точным расчетом и алгоритмом) методы принятия решений. В частности, при использовании ПИД-регулятора, можно использовать следующие закономерности:
- если переходный процесс имеет выраженный колебательный характер или на его графике имеется недопустимо большое перерегулирование, то необходимо усиливать воздействие по производной путем увеличения постоянной времени ТД Д–части ПИД-регулятора, ослаблять действие интегральной части путем увеличения постоянной времени ТИ И-части и ослаблять действие пропорциональной части путем уменьшения коэффициента передачи kП П-части;
- если ошибки регулирования (статическая, скоростная и т.д.) слишком велики, то необходимо усиливать действие пропорциональной части путем увеличения коэффициента передачи kП П-части и ослаблять в динамике действие интегральной части путем увеличения постоянной времени ТИ И-части;
- для повышения быстродействия САУ необходимо усиливать действие пропорциональной части путем увеличения коэффициента передачи kП П-части и усиливать в динамике действие интегральной части путем уменьшения постоянной времени ТИ И-части.
На рис.6.14 приведен пример сигнальной коррекции, где БАУ выполнен в виде пропорционального звена с большим коэффициентом передачи k.
Эквивалентная передаточная функция структурной схемы на рис.6.14,б при k →∞ имеет вид
 (6.6)
(6.6)
При k →∞ имеем:
 , так как
, так как 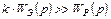
и  , так как
, так как

С учетом этих приближенных равенств преобразуем (6.6)


Значит, независимо от изменений параметров ОУ адаптивная САУ (рис.6.14,а) будет себя вести как звено с передаточной функцией WЭ (р).
Недостатком рассмотренной адаптивной САУ является то, что из-за очень большого коэффициента передачи k блока адаптивного управления в схеме появляется недопустимо большой сигнал Δи. На самом деле, сигнал Δи будет ограничен уровнями напряжения питания электронного блока адаптации. Поэтому вместо структурной схемы на рис.6.14,а корректно рассматривать структурную схему, приведенную на рис.6.15,а. Здесь БАУ реализовано на базе идеального двухпозиционного реле (компаратора), у которого при нулевом входном сигнале Δу коэффициент передачи равен бесконечности (k →∞), а при Δу≠0 выходной сигнал БАУ ограничен значениями ±Um. В этой САУ возникает скользящий режим, который характеризуется следующим:

- при Δу>0, когда выходной сигнал у объекта управления меньше эталонного уЭ, ко входу ОУ прикладывается большой положительный сигнал, равный Um, в результате чего сигнал у начинает интенсивно возрастать;
- в момент перехода значения Δу через ноль, после которого становится Δу<0, когда выходной сигнал у объекта управления больше эталонного уЭ, ко входу ОУ прикладывается большой отрицательный сигнал, равный -Um, в результате чего сигнал у начинает интенсивно уменьшаться.
Эти переключения сигнала Δи происходят с большой частотой так, что сигнал у в переходных процессах, вызванных переключениями БАУ, колеблется с малой амплитудой около сигнала уЭ, отслеживая любые изменения во времени последнего. Такие изменения у являются скольжением у вдоль линии уЭ (рис.6.15,б).
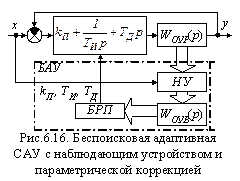 На рис.6.16 приведена обобщенная структурная схема адаптивной САУ, основанная на использовании восстановленной наблюдающим устройством модели объекта управления.
На рис.6.16 приведена обобщенная структурная схема адаптивной САУ, основанная на использовании восстановленной наблюдающим устройством модели объекта управления.
Объект управления имеет реальную передаточную функцию WОУР (р), параметры которой могут быть отличными от номинальных. Наблюдающее устройство параметров восстанавливает реальную передаточную функцию объекта управления WОУВ (р). В этой модели все параметры передаточной функции реальные, которые сложились у объекта управления на текущий момент времени. Блок расчета параметров БРП вычисляет по формулам, параметры kП, ТИ и ТД настройки регулятора и производит перестройку ПИД-регулятора. В этой схеме БАУ образуют наблюдающее устройство НУ, восстановленная модель объекта управления с передаточной функцией WОУВ (р) и блок расчета параметров БРП.
Вопросы и задания
1. Поясните работу беспоисковой адаптивной САУ с эталонной моделью исходной замкнутой САУ.
2. Поясните работу беспоисковой адаптивной САУ с пропорциональной сигнальной коррекцией.
3. Поясните работу беспоисковой адаптивной САУ с нелинейной (двухпозиционной) сигнальной коррекцией.
4. Поясните работу беспоисковой адаптивной САУ с наблюдающим устройством и параметрической коррекцией.
ЛИТЕРАТУРА
1. Березин С.Я., Тетюев Б.Я. Системы автоматического управления движением судна по курсу. - Л.: Судостроение, 1990. - 264 с.
2. Иващенко Н.Н. Автоматическое регулирование - М.: Машиностроение, 1978, 1980 г. – 736 с.
3. Ким Д.П. Теория автоматического управления. Т.1. Линейные системы. – М.: Физматлит, 2003. – 288 с.
4. Ким Д.П. Теория автоматического управления. Т.2. Многомерные, нелинейные, оптимальные и адаптивные системы. – М.: Физматлит, 2004. – 464 с.
5. Макаров И.М., Менский Б.М. Линейные автоматические системы - М.: Машиностроение, 1977. – 464 с.
6. Микропроцессорные автоматические системы регулирования / Под ред. В.В. Солодовникова. – М.: Высш. школа, 1991. –255 с.
7. Мирошник И.В. Теория автоматического управления. Линейные системы. СПб.: Питер, 2005. – 336 с.
8. Мирошник И.В. Теория автоматического управления. Нелинейные и оптимальные системы. СПб.: Питер, 2006. – 272 с.
9. Петров Ю.П. Оптимальное управление движением транспортных средств. – Л.: Энергия, 1969. – 96 с.
10. Петров Ю.П. Оптимальное управление электроприводом. – М-Л.: Госэнергоиздат, 1961. – 187 с.
11. Прохоренков А.М., Татьянченко Ю.Г., Солодов В.С. Судовая автоматика - М.: Колос, 1992. - 448 с.
12. Сборник задач по теории автоматического регулирования и управления / Под ред. В.А. Бессекерского. – М.: Высшая школа, 1982. – 587 с.
13. Суевалов Л.Ф. Справочник по расчетам судовых автоматических систем. - Л.: Судостроение, 1989. - 408 с.
ТАУ-1
1. Классификация САУ. Принципы автоматического управления
ЛИНЕЙНЫЕ САУ
2. Линеаризация элементов САУ. Преобразование Лапласа, передаточные функции. Типовые воздействия и реакция на них
3. Методы расчета переходных процессов, функции веса и построения графиков переходных процессов
4. Частотные характеристики линейных САУ
5. Логарифмические амплитудно-частотые характеристики – ЛАЧХ
6. Типовые позиционные звенья САУ
7. Типовые дифференцирующие звенья САУ
8. Типовые интегрирующие звенья САУ
9. Структурные схемы САУ и их преобразования
10. Понятие об устойчивости САУ. Прямые методы устойчивости. Критерий устойчивости Гурвица. Определение допустимых настроек САУ
11. Критерий устойчивости Михайлова. Определение допустимых настроек САУ
12. Критерий устойчивости Найквиста. Использование ЛАЧХ для оценки устойчивости САУ
13. Прямые показатели качества САУ. Расчет ошибок регулирования. Статические и астатические САУ
14. Косвенные показатели качества САУ и их связь с прямыми показателями качества. Использование ЛАЧХ для оценки качества САУ
15. Типовые законы регулирования. Влияние П-регулятора на показатели качества САУ
16. Типовые законы регулирования. Влияние И-регулятора на показатели качества САУ
17. Типовые законы регулирования. Влияние Д-регулятора на показатели качества САУ
18. Принципиальные электрические схемы типовых регуляторов
19. Схемы корректирующих устройств на пассивных элементах
20. Схемы корректирующих устройств на активных элементах
21. Коррекция линейных САУ с помощью местных обратных связей
22. Пример судовой линейной САУ
23. Сущность процесса синтеза САУ. Частотный метод синтеза линейных САУ
САУ СО СЛУЧАЙНЫМИ СИГНАЛАМИ
24. Типы случайных процессов и их характеристики
25. Прохождение стационарного случайного сигнала через линейное звено
26. Расчет ошибок регулирования в линейной САУ при воздействии на нее полезного сигнала с помехой
27. Пример судовой САУ, отрабатывающей полезный сигнал с помехой
ТАУ-2
НЕЛИНЕЙНЫЕ САУ
1. Определение нелинейных САУ. Анализ нелинейных САУ методом припасовывания
2. Определение и свойства фазовых траекторий. Фазовые траектории линейных САУ 2-го порядка
3. Расчет фазовым методом нелинейной САУ 2-го порядка с идеальным трехпозиционным реле
4. Расчет фазовым методом нелинейной САУ 2-го порядка с гистерезисным двухпозиционным реле
5. Расчет фазовым методом нелинейной САУ 1-го порядка с гистерезисным двухпозиционным реле
6. Нелинейная САУ с переменной структурой
7. Нелинейная САУ со скользящим режимом
8. Метод гармонической линеаризации. Коэффициенты гармонической линеаризации
9. Исследование нелинейных САУ методом гармонической линеаризации
10. Устойчивость нелинейных САУ
ИМПУЛЬСНЫЕ САУ
11. Импульсные и цифровые САУ. Виды модуляции непрерывных сигналов
12. Схемы импульсных модуляторов
13. Способы описания импульсных сигналов. Особенности соответствия оригиналов и изображений
14. Дискретные передаточные функции звеньев
15. Дискретные передаточные функции разомкнутых и замкнутых импульсных САУ
16. Методы расчета переходных процессов в импульсных САУ
17. Устойчивость импульсных САУ
18. Синтез корректирующих устройств и регуляторов импульсных САУ
19. Реализация микропроцессорных корректирующих устройств по заданным дискретным передаточным функциям
20. Определение дискретных передаточных функций микропроцессорных устройств, реализующих работу непрерывных устройств
ОПТИМАЛЬНЫЕ САУ
21. Постановка задач оптимального управления. Вариационные методы теории оптимальных САУ
22. Оптимальное управление ДПТ с независимым возбуждением при постоянном моменте сопротивления
23. Оптимальное управление ДПТ с независимым возбуждением при ограничениях на частоту вращения и ток якоря
24. Оптимальное управление ДПТ с независимым возбуждением при моменте сопротивления, зависящем от частоты вращения и времени
25. Оптимальное управление ДПТ с независимым возбуждением при моменте сопротивления, зависящем от угла поворота вала
26. Оптимальное управление асинхронным двигателем в установившемся режиме
27. Оптимальное по минимуму расхода топлива управление движением судна
28. Методы оптимального управления, основанные на принципе максимума Понтрягина
29. Оптимальное управление объектом 2-го порядка при ограничении на величину сигнала управления
30. Оптимальное управление синхронными генераторами электростанции по критерию устойчивости
АДАПТИВНЫЕ САУ
31. Назначение и классификация адаптивных САУ. Структура и принцип действия самонастраивающихся систем
32. Методы определения градиента целевой функции
33. Организация рабочих операций в экстремальной САУ
34. Пример экстремальной САУ асинхронного электропривода по минимуму потребляемого тока
35. Структура и принцип действия беспоисковых адаптивных САУ
ТАУ-1
1. Классификация САУ. Принципы автоматического управления
ЛИНЕЙНЫЕ САУ
2. Линеаризация элементов САУ. Преобразование Лапласа, передаточные функции. Типовые воздействия и реакция на них
3. Методы расчета переходных процессов, функции веса и построения графиков переходных процессов
4. Частотные характеристики линейных САУ
5. Логарифмические амплитудно-частотые характеристики – ЛАЧХ
6. Типовые позиционные звенья САУ
7. Типовые дифференцирующие звенья САУ
8. Типовые интегрирующие звенья САУ
9. Структурные схемы САУ и их преобразования
10. Понятие об устойчивости САУ. Прямые методы устойчивости. Критерий устойчивости Гурвица. Определение допустимых настроек САУ
11. Критерий устойчивости Михайлова. Определение допустимых настроек САУ
12. Критерий устойчивости Найквиста. Использование ЛАЧХ для оценки устойчивости САУ
13. Прямые показатели качества САУ. Расчет ошибок регулирования. Статические и астатические САУ
14. Косвенные показатели качества САУ и их связь с прямыми показателями качества. Использование ЛАЧХ для оценки качества САУ
15. Типовые законы регулирования. Влияние П-регулятора на показатели качества САУ
16. Типовые законы регулирования. Влияние И-регулятора на показатели качества САУ
17. Типовые законы регулирования. Влияние Д-регулятора на показатели качества САУ
18. Принципиальные электрические схемы типовых регуляторов
19. Схемы корректирующих устройств на пассивных элементах
20. Схемы корректирующих устройств на активных элементах
21. Коррекция линейных САУ с помощью местных обратных связей
22. Пример судовой линейной САУ
23. Сущность процесса синтеза САУ. Частотный метод синтеза линейных САУ
САУ СО СЛУЧАЙНЫМИ СИГНАЛАМИ
24. Типы случайных процессов и их характеристики
25. Прохождение стационарного случайного сигнала через линейное звено
26. Расчет ошибок регулирования в линейной САУ при воздействии на нее полезного сигнала с помехой
27. Пример судовой САУ, отрабатывающей полезный сигнал с помехой
ТАУ-2
НЕЛИНЕЙНЫЕ САУ
1. Определение нелинейных САУ. Анализ нелинейных САУ методом припасовывания
2. Определение и свойства фазовых траекторий. Фазовые траектории линейных САУ 2-го порядка
3. Расчет фазовым методом нелинейной САУ 2-го порядка с идеальным трехпозиционным реле
4. Расчет фазовым методом нелинейной САУ 2-го порядка с гистерезисным двухпозиционным реле
5. Расчет фазовым методом нелинейной САУ 1-го порядка с гистерезисным двухпозиционным реле
6. Нелинейная САУ с переменной структурой
7. Нелинейная САУ со скользящим режимом
8. Метод гармонической линеаризации. Коэффициенты гармонической линеаризации
9. Исследование нелинейных САУ методом гармонической линеаризации
10. Устойчивость нелинейных САУ
ИМПУЛЬСНЫЕ САУ
11. Импульсные и цифровые САУ. Виды модуляции непрерывных сигналов
12. Схемы импульсных модуляторов
13. Способы описания импульсных сигналов. Особенности соответствия оригиналов и изображений
14. Дискретные передаточные функции звеньев
15. Дискретные передаточные функции разомкнутых и замкнутых импульсных САУ
16. Методы расчета переходных процессов в импульсных САУ
17. Устойчивость импульсных САУ
18. Синтез корректирующих устройств и регуляторов импульсных САУ
19. Реализация микропроцессорных корректирующих устройств по заданным дискретным передаточным функциям
20. Определение дискретных передаточных функций микропроцессорных устройств, реализующих работу непрерывных устройств
ОПТИМАЛЬНЫЕ САУ
21. Постановка задач оптимального управления. Вариационные методы теории оптимальных САУ
22. Оптимальное управление ДПТ с независимым возбуждением при постоянном моменте сопротивления
23. Оптимальное управление ДПТ с независимым возбуждением при ограничениях на частоту вращения и ток якоря
24. Оптимальное управление ДПТ с независимым возбуждением при моменте сопротивления, зависящем от частоты вращения и времени
25. Оптимальное управление ДПТ с независимым возбуждением при моменте сопротивления, зависящем от угла поворота вала
26. Оптимальное управление асинхронным двигателем в установившемся режиме
27. Оптимальное по минимуму расхода топлива управление движением судна
28. Методы оптимального управления, основанные на принципе максимума Понтрягина
29. Оптимальное управление объектом 2-го порядка при ограничении на величину сигнала управления
30. Оптимальное управление синхронными генераторами электростанции по критерию устойчивости
АДАПТИВНЫЕ САУ
31. Назначение и классификация адаптивных САУ. Структура и принцип действия самонастраивающихся систем
32. Методы определения градиента целевой функции
33. Организация рабочих операций в экстремальной САУ
34. Пример экстремальной САУ асинхронного электропривода по минимуму потребляемого тока
35. Структура и принцип действия беспоисковых адаптивных САУ
Ó Дворак Николай Маркович
Поиск по сайту: