 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Числовой пример
Пусть ДПФ разомкнутой САУ имеет вид (4.17)

ДПФ замкнутой САУ в соответствии с формулой (4.21) будет следующей
 (4.22)
(4.22)
Вопросы и задания
1. Какова эквивалентная ДПФ последовательно соединенных звеньев? Как на расчет эквивалентной ДПФ влияет вид сигнала, которым связаны звенья последовательной цепи?
2. Какова эквивалентная ДПФ параллельно соединенных звеньев?
3. Какова эквивалентная ДПФ соединения звеньев с обратной связью?
4. Поясните вычисления дискретной передаточной функции, приведенные в примере.
4.6. Методы расчета переходных процессов
в импульсных САУ
По определению (см. тема 2) переходным процессом называется реакция САУ на единичный скачок.
Если  - z -изображение входного сигнала САУ и WЗАМ (z) – ДПФ импульсной САУ, то в соответствии с определением ДПФ (41.9), z -изображение переходного процесса будет иметь вид
- z -изображение входного сигнала САУ и WЗАМ (z) – ДПФ импульсной САУ, то в соответствии с определением ДПФ (41.9), z -изображение переходного процесса будет иметь вид
 (4.23)
(4.23)
Далее методы расчета изучим на числовых примерах.
При WЗАМ (z) вида (4.22) z -изображение переходного процесса будет следующим
 (4.24)
(4.24)
Расчет переходного процесса в импульсной САУ состоит в определении амплитуд импульсов выходного сигнала h (z) или, что эквивалентно, - расчет решетчатой функции h (n). Существуют два метода расчета:
1) метод разложения h (z) в ряд по степеням z-n;
2) табличный метод.
1. Метод разложения (распаковки) h (z) в ряд по степеням z-n
Преобразуем (43.2) к стандартному виду

Выполним деление многочлена 0,5z2-0,35z на многочлен z2-1,8z+0,8

Результатом деления является ряд
 , (4.25)
, (4.25)
коэффициентами которого при степенях z-n являются значения решетчатой функции h (n) переходного процесса (см. (4.8)).
Заполним табл.4.2 и построим график переходного процесса (рис.4.20).
Таблица 4.2
Значения решетчатой функции переходного процесса
| Номер импульса п | ∞ | ||||||||||
| h (n) из ряда (4.25) | 0,5 | 0,55 | 0,59 | ||||||||
| h (n) из формулы (4.28) | 0,5 | 0,55 | 0,59 | 0,622 | 0,648 | 0,668 | 0,684 | 0,698 | 0,708 | 0,716 | 0,75 |
Достоинством метода является непосредственное определение решетчатой функции h (п) из выражения h (z) при минимуме предварительных его преобразований h (z).
 Недостатком метода является то, что при заранее неизвестном установившемся значении решетчатой функции h (п) является неопределенным число необходимых делений двух многочленов.
Недостатком метода является то, что при заранее неизвестном установившемся значении решетчатой функции h (п) является неопределенным число необходимых делений двух многочленов.
2. Табличный метод
Преобразуем (4.24) к сумме табличных z -выражений (табл.4.1)
 (4.26)
(4.26)
Для определения коэффициентов А и В составляем и решаем систему уравнений

Подставляем А и В в (4.26), и, используя табл.4.1, находим оригинал h (t)
 , (4.27)
, (4.27)
где α должно быть таким, чтобы было (см. табл.4.1)

В выражении (4.27) нужно брать дискретное время, значения которого совпадают с периодом Т следования импульсов:
 (4.28)
(4.28)
Вычисления h (п) по формуле (4.28) даёт те же значения решетчатой функции, которые были определены 1-м методом (табл.4.2).
Имея формулу выражения переходного процесса, можно определить установившееся значение переходного процесса и его длительность в импульсах.

Для расчета длительности переходного процесса преобразуем (4.28)

Длительность переходного процесс в импульсах находим из уравнения

Вопросы и задания
1. Как рассчитать z-изображение переходного процесса?
2. Поясните метод расчета переходного процесса разложением в ряд.
3. Поясните табличный метод расчета переходного процесса.
4. Как рассчитать установившееся значение и продолжительность переходного процесса?
4.7. Устойчивость импульсных САУ
Устойчивость импульсных САУ можно оценивать прямым методом и с использованием критериев.
Прямой метод оценки устойчивости заключается в расчете и построении графика переходного процесса: для устойчивой САУ значение h (∞) должно быть конечной величиной, которое называется установившемся значением hуст переходного процесса. Однако расчет и построение графика являются достаточно трудоемкими операциями.
Несколько проще суждение об устойчивости может быть вынесено на основе анализа корней zi характеристического уравнения ДПФ (характеристическое уравнение составляется путем приравнивания к нулю знаменателя ДПФ замкнутой САУ). Эти корни определяют значения параметра di (см. табл.40.1), равного, соответственно, для устойчивого экспоненциального и затухающего колебательного процессов
 (4.29)
(4.29)
Значение αi затем входит в показатель экспоненты выражения оригинала h (t). САУ будет устойчива, если значения αi для всех корней zi будет положительным, а, согласно (4.29), все корни zi характеристического уравнения по модулю меньше 1:  .
.
Прямые методы имеют тот недостаток, что позволяют судить об устойчивости для САУ с невысоким порядком характеристического многочлена ДПФ (не выше 2-го порядка). В общем случае задача оценки устойчивости проще решается с помощью критериев устойчивости.
После соответствующих преобразований выражения ДПФ оценка устойчивости может быть произведена критериями Гурвица, Михайлова, Найквиста. Рассмотрим применение критерия Гурвица, который базируется на анализе характеристического многочлена D (z) ДПФ замкнутой импульсной САУ. Предварительно в D (z) производится следующая замена
 (4.30)
(4.30)
Данная замена обладает тем свойством, что при | z | <1 переменная w имеет отрицательную действительную часть (Re (w)< 0), что доказывается следующими преобразованиями:


Следовательно, выражение D (w) должно быть проверено на отрицательность действительных частей его корней. Это как устанавливается с использованием критериев устойчивости Гурвица, Михайлова, Найквиста и др.
Примеры:
1. Исследуем с использованием критерия Гурвица устойчивость импульсной САУ, если ее ДПФ имеет 1-й порядок

Решение.
В характеристическом многочлене D (z) =z-a выполняем замену (4.30):

В соответствии с критерием Гурвица САУ 1-го порядка устойчива, если все коэффициенты характеристического многочлена D (w) положительны

2. Исследуем на устойчивость импульсную САУ, если ее ДПФ имеет 2-й порядок

Решение.
В характеристическом многочлене D(z)=z-a выполняем замену (44.2)

В соответствии с критерием Гурвица САУ 2-го порядка устойчива, если все коэффициенты числителя многочлена D (w) положительны
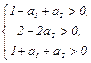 (4.31)
(4.31)
Графическое решение системы неравенств (4.31) показано на рис.4.21. Область устойчивости отмечена штриховкой.

Вопросы и задания
1. При каких значениях корней характеристического уравнения ДПФ импульсная САУ будет устойчивой?
2. Почему неприменимы критерии устойчивости Гурвица, Михайлова и Найквиста к характеристическому многочлену D ( z ), а к характеристическому многочлену D ( w ) применимы?
3. При каких значениях коэффициентов характеристического многочлена ДПФ 1-го порядка САУ устойчива?
4. При каких значениях коэффициентов характеристического многочлена ДПФ 2-го порядка САУ устойчива?
4.8. Синтез корректирующих устройств
и регуляторов импульсных САУ
Одним из требований к САУ может быть формирование заданного графика решетчатой функции переходного процесса. Так в рассчитанный в теме 4.6 переходный процесс при заданной передаточной функции непрерывной части WИЧ (р) имеет следующие недостатки:
 1) установившаяся ошибка регулирования составляет 25%, что, безусловно, очень много;
1) установившаяся ошибка регулирования составляет 25%, что, безусловно, очень много;
2) длительность переходного процесса составляет 9 тактов, что также является слишком большой величиной.
В импульсных САУ достаточно прост синтез корректирующего устройства, с которым в САУ устанавливается желаемый переходный процесс. Процесс синтеза, для большей его наглядности, рассмотрим на числовом примере. Структурная схема синтезированной САУ имеет стандартный вид (рис.4.22). В качестве корректирующего устройства выберем микропроцессорное. Это устройство работает с амплитудно-модулированными импульсными на входе и выходе (см. рис.4.5), поэтому условия для использования формулы (4.18) выполняются.
 Задаемся графиком желаемого переходного процесса hЖ (п) (рис.4.23), у которого ошибка регулирования составляет 0%, а длительность переходного процесса составляет 2 такта.
Задаемся графиком желаемого переходного процесса hЖ (п) (рис.4.23), у которого ошибка регулирования составляет 0%, а длительность переходного процесса составляет 2 такта.
Значения решетчатой функции hЖ (п) графика желаемого переходного процесса заносим в табл.4.3. Далее вычисляем значения решетчатой функции εЖ (п) =1 (п) -hЖ (п) (формула следует из рис.4.22) графика желаемой ошибки регулирования и также заносим в табл.4.3.
Таблица 4.3
Данные для желаемых графиков hЖ(п) и εЖ(п)
| Номер п импульса | … ∞ | ||||
| Значения желаемого графика hЖ (п) | 0,8 | ||||
| Значения желаемого графика εЖ (п) | 0,2 |
Значение εЖ (п) содержат конечное число ненулевых элементов и бесконечное – нулевых. Используя представление z -изображения в виде ряда (см. (4.8)), по данным табл.4.3 запишем для εЖ (п) конечный ряд


Запишем, используя hЖ (z) =1 (z) -εЖ (z), z -изображение для сигнала hЖ (z):

Используя определение ДПФ (см. (4.14)), определяем желаемую ДПФ разомкнутой САУ

Так как согласно структурной схемы, изображенной на рис.45.1,
 ,
,
то ДПФ корректирующего устройства будет иметь вид
 (4.32)
(4.32)
где WНЧ (z) взято равным выражению (4.17) ДПФ непрерывной части разомкнутой САУ.
Если график желаемого переходного процесса hЖ (п) будет иметь конечное число ненулевых значений и бесконечное – нулевых (рис.4.24), то сначала составляется выражение hЖ (z) в виде конечного ряда, а затем вычисляется εЖ (z) =1 (z) -hЖ (z).
Вопросы и задания
1. Как на основании желаемого графика переходного процесса составить z-изображения выходного сигнала САУ и сигнала ошибки?
2. Как рассчитать ДПФ корректирующего устройства импульсной САУ, обеспечивающей желаемый график переходного процесса?
4.9. Реализация микропроцессорных корректирующих
устройств по заданным дискретным передаточным функциям
Пусть z -изображение для сигнала х (z) имеет вид ряда

Образуем смещенное на т тактов вправо z -изображение, умноженное на ат,

Ограничимся, для определенности, исходным и смещенными на 1 и 2 такта изображениями, и построим их графики x (n), a1x (n) z-1 и a2x (n) z-2 (рис.4.25).
Суммой исходного и смещенных z -изображений является выражение
 (4.33)
(4.33)
Представим z -изображение суммы S(z) в виде ряда

Пользуясь построениями, приведенными на рис.4.25, рассчитаем всего одно значение решетчатой функции суммы S (z)

или, обобщая для произвольного п -го такта, получим
 ,
,
причем значения решетчатой функции для тактов с отрицательными номерами (х (-1), х (-2) и т.д.) принимаются равными нулю.
Из сопоставления выражений z -изображения суммы S (z) (4.33) и значения решетчатой функции суммы S (п) для любого п- го такта (4.34) видно, что:
1) в выражение суммы (4.34) входят только значения решетчатой функции исходного сигнала (х (п), х (п-1), х (п-2)и т.д.), взятые с такими номерами импульсов, которые смещены влево (назад) относительно п -го импульса на количество тактов, равное показателю степени у оператора z в выражении S (z) (4.33);

2) коэффициенты а1, а2 и т.д. из выражения S (z) (4.33) переходят на соответствующие места в выражении суммы S (п).
На основании изложенного можно осуществлять переход от ДПФ корректирующего устройства к вычислениям над его входными и выходными импульсами по, так называемым, разностным уравнениям. Для наглядности рассмотрим числовой пример.
Пример
Пусть ДПФ корректирующего устройства имеет вид (4.32).
Составим разностное уравнение для расчета текущего значения выходного импульса и (п) корректирующего устройства.
Решение
1. Приведем выражение (4.32), поделив числитель и знаменатель его на z в максимальной степени:

2. Составим операторное уравнение корректирующего устройства

3. Осуществляем переход к уравнению над значениями решетчатых функций сигналов u (z) и ε (z)

Получено разностное уравнение, связывающее арифметическими действиями входные и выходные импульсы корректирующего устройства.
4. Текущее значение выходного сигнала и (п) корректирующего устройства вычисляется по выражению
 (4.35)
(4.35)
Структура выражения (4.35) показывает, что для определения текущего значения выходного сигнала и (п) корректирующего устройства необходимо взять предшествующие значения выходного и (п-1) и входного ε (п-1) сигналов, предшествующие на 2 такта значения и (п-2) и ε (п-2) и предшествующие на 3 такта значения и (п-3) и ε (п-3) и выполнить над ними вычисления. Предшествующие значения необходимо хранить в оперативном запоминающем устройстве микропроцессорного управляющего устройства.
5. Алгоритм вычислений и (п) по (4.35) является циклическим и имеет вид, приведенный на рис.4.26.

Вопросы и задания
1. Дайте определение смещенной решетчатой функции и их сумме.
2. Выведите формулу для вычисления значения произвольного п-го импульса решетчатой функции суммы смещенных сигналов.
3. Что такое "разностное уравнение" и как оно выводится из ДПФ корректирующего устройства?
4. Поясните алгоритм работы корректирующего устройства.
4.10. Определение дискретных передаточных функций
микропроцессорных устройств, реализующих
работу непрерывных устройств
Применяемые в непрерывных САУ регуляторы, корректирующие устройства, фильтры, фазовращатели и другие устройства могут быть реализованы не только на непрерывных элементах, но и на микропроцессорной технике. Для микропроцессорной реализации непрерывных устройств необходимо рассчитать их ДПФ так, как это было рассмотрено в теме 4.4, и дальше выйти на разностное уравнение так, как это было рассмотрено в теме 4.9. Этим путем можно получить разностное уравнение, которым точно воспроизводится процедура преобразования входного сигнала устройства в выходной его сигнал при любом законе изменения входного сигнала.
Однако этот путь является громоздким, требующем объемных расчетов и преобразований. В практике проектирования микропроцессорных систем автоматики охотнее пользуются более простым методом, хотя расчеты по нему имеют погрешность. Суть метода состоит в прямом переходе, минуя z- изображения, от дифференциальных уравнений, описывающих работу устройства. к разностному. Ниже на двух примерах рассмотрен этот метод. Результаты легко обобщаются на любые другие устройства.
1. Микропроцессорная реализация ПИ-регулятора
Передаточная функция W (p) ПИ-регулятора, его дифференциальное уравнение и переходный процесс u (t):
 (4.36)
(4.36)
 (4.37)
(4.37)
Точное определение производной  содержит предельный переход по переменной t, изменение которой Δt стремится к нулю. В импульсных САУ шаг изменения времени ограничен периодом Т следования импульсов. Поэтому производная может быть определена только приближенно
содержит предельный переход по переменной t, изменение которой Δt стремится к нулю. В импульсных САУ шаг изменения времени ограничен периодом Т следования импульсов. Поэтому производная может быть определена только приближенно

 , (4.38)
, (4.38)
где ип – текущее и ип-1 – предшествующее значения сигнала и.
Применим (4.38) к дифференциальному уравнению (4.36)
 , (4.39)
, (4.39)
откуда получим формулу для вычисления текущего значения ип выходного импульса ПИ-регулятора в микропроцессорном исполнении
 (4.40)
(4.40)
Выражение (4.40) является, по существу, разностным уравнением, воспроизводящем дискретно работу ПИ-регулятора. Явственно видно, что вывод разностного уравнения при исходно заданной непрерывной передаточной функции гораздо проще, чем вывод с использованием z -изображений. Но при проделанном выводе была использована всего лишь одна приближенная замена (4.38) непрерывной производной на ее дискретный аналог. Поэтому, следует ожидать, что и разностное уравнение (4.40) также будет неточным.
Для оценки погрешности в работе ПИ-регулятора от приближенного определения производной по (4.38), рассчитаем переходный процесс для микропроцессорного ПИ-регулятора и сравним его точным переходным процессом (4.37). Особенностью вычислений текущего значения сигнала ип по формуле (4.40) является то, что ип вычисляется рекуррентно, через предшествующие значения сигналов и и ε. С таким выражением ип невозможно оценить погрешность работы дискретного ПИ-регулятора. Нужно перейти от рекуррентных вычислений к формульным, в которых значение ип рассчитывалось бы в функции номера п импульса.
Вывод формулы для вычисления сигнала ип в функции п выполним на примере, когда на входе ПИ-регулятора действует сигнал единичного скачка со значениями входных импульсов с момента времени t=0
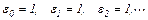
До момента t=0, естественно, нужно считать, что  .
.
Вычисления значений выходного сигнала ип ПИ-регулятора при п=0, 1, 2,… проводим по формуле (4.40):
| Номер п импульса | Вычисления ип | |
| 0 | u0 = 0 + bT +a (1-0) =a+bT | |
| 1 | u1 = u0 + bT +a (1-1) =a+bT+bT | |
| 2 | u2 = u1 + bT +a (1-1) =a+bT+2bT | (4.41) |
| : | : | |
| п-1 | un-1 = un-2 + bT +a (1-1) =a+bT+ (n-1) bT | |
| п | un = un-1 + bT +a (1-1) =a+bT+nbT |
В последней строке системы (4.41) содержится искомая формула для вычисления сигнала ип в функции номера п импульса.
Теперь рассчитаем решетчатую функцию для выходного сигнала (4.37) непрерывного ПИ-регулятора. Эта решетчатая функция получается при замене в (4.37) непрерывного времени t на дискретное время пТ:

Графики переходных процессов для непрерывного uп (t) и импульсного un ПИ-регуляторов построены на рис.4.27. Отличаются графики друг от друга на величину ип-ип (t)= a+bT+nbT- a+bnT=bT. Это и есть величина погрешности работы дискретного ПИ-регулятора.
Для уменьшения этой погрешности нужно уменьшать как параметр b, так и период Т следования импульсов. Параметр b обратно пропорционален постоянной времени ТИ интегральной части ПИ-регулятора. Поэтому с увеличением ТИ различие между графиками un (t) и un уменьшается.
Следует отметить, что погрешность величиной bT возникает при отработке ПИ-регулятором входного сигнала типа единичного скачка. При другом входном сигнале, погрешность также будет другой, причем существуют следующая закономерность – с увеличением скорости изменения входного сигнала погрешность интегратора также возрастает. Для дискретного ПИ-регулятора. рассчитанного с использованием z -изображений, такой зависимости погрешности от скорости изменения входного сигнала не существует.
2. Микропроцессорная реализация фильтра низкой частоты (ФНЧ)
ФНЧ пропускает сигналы низких частот и задерживает сигналы высоких частот. Схема ФНЧ 2-го порядка на аналоговых элементах приведена на рис.4.28. Передаточная функция и дифференциальное уравнение фильтра имеют вид
 (4.42)
(4.42)

Вторая производная в дискретном варианте будет иметь вид
 (4.43)
(4.43)
Подставляем в (4.42) выражения (4.38) и (4.43). Получаем разностное уравнение

откуда может быть найдено текущее значение ип выходного сигнала ФНЧ.
В заключение следует отметить, что для дискретных устройств, воспроизводящих работу непрерывных, независимо от того, каким методом получены их разностные уравнения, погрешность их работы можно уменьшить путем увеличения частоты следования импульсов  или, что эквивалентно, уменьшения периода Т их следования.
или, что эквивалентно, уменьшения периода Т их следования.
Вопросы и задания
1. Назовите методы вывода разностных уравнений, воспроизводящих работу непрерывных устройств. Перечислите достоинства и недостатки методов и сформулируйте области их применения.
2. Как выводятся разностные уравнения непосредственно из дифференциальных уравнений 1-го порядка, описывающих непрерывные устройства? Из-за чего возникает погрешность вывода разностного уравнения?
3. Как оценить величину погрешности работы дискретного устройства? Почему для получения оценки погрешности нужно иметь формулу для вычисления выходного сигнала дискретного устройства в функции его номера?
4. От чего зависит погрешность работы дискретного устройства и как её можно уменьшить?
5. Как выводятся разностные уравнения непосредственно из дифференциальных уравнений 2-го порядка, описывающих непрерывные устройства? Из-за чего возникает погрешность вывода разностного уравнения?
5. ОПТИМАЛЬНЫЕ САУ
5.1. Постановка задач оптимального управления.
Вариационные методы теории оптимальных САУ
Оптимальными называются САУ, которые обеспечивают регулирование, доставляющее экстремум показателям качества, например, работа с максимальной производительностью, минимальным потреблением энергии, максимальным к.п.д. и т.д. Указанную суть оптимальных САУ и особенности постановки и решения задач оптимальных САУ рассмотрим на примере нескольких простейших примеров.
1. Задача о кратчайшем расстоянии (min L) между двумя точками (рис.5.1).

Между двумя точками может быть бесконечное множество траекторий (маршрутов), каждой из которых можно сопоставить обобщенную характеристику L – длину траектории. На плоскости (рис.5.1а) ответ очевиден: из всех возможных траекторий 1, 2 или 3 кратчайшей будет прямая линия 2. Если между точками А и В имеется препятствие, например, холм (рис.5.1б), то очевидно только то, что по прямой линии движение невозможно, а определение кратчайшей линии, которая будет состоять из прямых и криволинейных отрезков, проходящих по склону холма, является сложной для решения задачей.
2. Задача о форме провисающей цепи корабельного якоря, форме провисающих проводов линии электропередачи и т.п. Оказывается, что провисающие якорная цепь, провода и т.п. всегда принимают такую форму, при которой сумма W потенциальных энергий элементарных масс цепи или провода принимает минимальное значение (min W), т.е. изменение формы цепи или провода происходит до тех пор, пока это понижает их потенциальную энергию.
3. Задача об управлении электродвигателем по максимуму к.п.д. Необходимо найти такой закон изменения напряжения его питания, чтобы в процессе выполнения заданного объема работы были бы минимальны тепловые потери в его обмотках. Такое управление максимизирует к.п.д.
Решение рассмотренных задач не элементарно, а основано на строгих математических теориях, в которых обязательными компонентами являются аргумент и функция. В математической постановке задач оптимального управления содержание и смысл аргумента и функции отличается от аналогичных понятий, используемых в классической высшей математике. В классической высшей математике связь между аргументом х и функцией у является точечной, а именно: числовому значению аргумента сопоставляется числовое значение аргумента в виде аналитической функции y=f (x). В задачах оптимального управления аргументом является формула, которая является аналитическим (формульным) описанием траектории (в рассмотренной задаче 1), линии (в задаче 2), закона изменения во времени (в задаче 3) и т.п. Функцией является число (точечное значение), которое является обобщенной характеристикой формульного аргумента: длина пути в задаче 1, потенциальная энергия в задаче 2, величина потерь энергии в задаче 3 и т.п.
Связь между формульным аргументом и числовой функцией называется функциональной связью, а аналитическая запись этой связи называется функционалом.
В качестве функционала чаще всего используют определенный интеграл
 (5.1)
(5.1)
Подинтегральное выражение F является аргументом функционала и одновременно функцией от точечных аргументов, например,  . Сам же интеграл J является числом, что подходит под определение функции функционала.
. Сам же интеграл J является числом, что подходит под определение функции функционала.
Смысл решения задач оптимального управления состоит в определении такой аналитической зависимости y=f (t), при которой значение функционала J экстремально – минимально или максимально. Определенное таким образом решение называется экстремалью. Так, в задаче 1 необходимо найти такое аналитическое описание траектории, у которой длина будет минимальна, в задаче 2 необходимо найти такую форму провисающей цепи, чтобы потенциальная энергия цепи была бы минимальна, в задаче 3 необходимо найти такой закон изменения во времени питающего напряжения, чтобы тепловые потери в электродвигателе были бы минимальны и т.п.
Для решения задач оптимального управления существуют специальные математические методы. Ниже будут рассмотрены два самых распространенных метода: классический вариационный метод и метод принципа максимума Понтрягина.
Основные формулы и теоремы вариационного исчисления
Вариационное исчисление позволяет отыскивать экстремали функционала,
Основной теоремой вариационного исчисления является теорема Эйлера: если функция у=у (t) доставляет экстремум интегралу J, то она должна удовлетворять следующему дифференциальному уравнению (уравнению Эйлера):
 (5.2)
(5.2)
Решение уравнения Эйлера называется экстремалью.
Применим уравнение Эйлера для определения формы линии на плоскости (рис.5.1а), которая кратчайшим способом соединяет две точки – А и В.
Длина элементарного участка траектории согласно рис.5.1а равна

Длина всей линии
 . Здесь
. Здесь 
Находим частные производные от F и производную по аргументу х
 (5.3)
(5.3)
Подставляем (5.3) в уравнение Эйлера (5.2)
 ,
,
откуда


Это уравнение прямой линии, соединяющей точки А и В. Постоянные интегрирования находятся из условия прохождения прямой чрез точки А и В.
В общем случае уравнение Эйлера является дифференциальным уравнением второго порядка, и в решение его входят две произвольные постоянные. Эти произвольные постоянные должны быть определены из граничных условий. Простейшим случаем граничных условий является условие, чтобы кривая у (t) проходила через две заданные точки:  .
.
В частных случаях уравнение Эйлера может превращаться в дифференциальное уравнение 1-го порядка, или даже в уравнение, не содержащее производных. Соответственно должно уменьшаться и число задаваемых граничных условий.
Уравнение Эйлера является необходимым, но не достаточным условием, т.е. функции, удовлетворяющие уравнению (5.2), в некоторых случаях могут не доставлять экстремума. Для того чтобы решения уравнения Эйлера доставляли экстремум функционалу (5.1), достаточно, чтобы они не имели самосопряженных точек (условие Якоби) и выполнялось условие (Лежандра):
 - для минимума и
- для минимума и  - для максимума функционала (5.1).
- для максимума функционала (5.1).
Задача о разыскании экстремума функционала (5.1) является простейшей задачей вариационного исчисления. Существуют обобщения (варианты) вариационных задач, постановка которых несколько шире простейшей.
Первым обобщением простейшей задачи является пространственная задача, когда функционал зависит от нескольких функций у1, у2, … (в классическом понимании), входящих в подинтегральную функцию F (функция F является аргументом функционала)
 (5.4)
(5.4)
В этом случае нам нужно найти п функций от t, т.е. у1, у2…уn, которые при подстановке в (5.4) доставят экстремум функционалу J. Эти функции находятся из системы п уравнений Эйлера:

Другим (особенно нужным для задач автоматического управления) обобщением простейшей задачи вариационного исчисления является задача на условный экстремум, когда функции yi (t), входящие в функционал (5.4), должны удовлетворять еще некоторым добавочным условиям. Наиболее общим случаем задачи на условный экстремум является общая задача Лагранжа, когда n функций у1, у2,…, уn, доставляющих максимум функционалу (5.4), удовлетворяют еще системе, состоящей из k интегральных, m дифференциальных и l алгебраических выражений:
 |
(5.5)
В этом случае составляется m уравнений Эйлера для промежуточной функции L, определяемой равенством:
 (5.6)
(5.6)
где λ1, λ2,…,λk – постоянные числа, а λk+1 (t),…, λk+m+l (t) - произвольные функции от t. Итого для определения n функций у и k+m+l функций λ (t) имеем систему из n+m+k+l уравнений: n уравнений Эйлера и k+m+l уравнений (5.6).
Следующим обобщением простейшей задачи вариационного исчислений является задача отыскания экстремума функционала, зависящего не только от первой, но и от старших производных искомой функции:

решение ищем из уравнения Эйлера—Пуассона:
 ,
,
которое является в общем случае дифференциальным уравнением порядка 2n. Для полного определения искомой функции у (t) необходимы 2n граничных условий, которые могут быть заданы, например, путем задания значений функции у (t) и (п-1) ее производных в точках t1 и t2.
Самым сложным обобщением простейшей задачи вариационного исчисления является задача, в которой на искомую функцию у (t) накладываются дополнительные ограничения в виде неравенств.
Заданное неравенство или система неравенств ограничивают некоторую область, и искомая функция у (t), доставляющая экстремум, может заключаться только внутри этой допустимой области и не может выходить за ее пределы.
Поэтому при решении этой задачи (называемой часто задачей на ограниченную вариацию) могут встретиться следующие три возможности:
1. Решение уравнения Эйлера целиком находится внутри допустимой области и нигде не выходит за ее пределы. В этом случае искомая функция целиком определяется уравнением Эйлера, и наличие неравенств на решение не влияет.
2. Решение уравнения Эйлера целиком находится вне допустимой области. В этом случае экстремальное значение функционала (5.1) будет достигаться тогда, когда функцией у (t), входящей в (5.1), будет являться граница допустимой области. Решением будет граничная кривая.
3. Решение уравнения Эйлера пересекает границу допустимой области. В этом случае экстремум будет достигаться на кривой, "склеенной" из кусков экстремалей и кусков граничных кривых.
Наиболее сложным для исследования является третий случай. В нем мы должны не только найти уравнения экстремалей и уравнения границы допускаемой области, но и координаты точек "склеивания". Найти эти точки помогает следующая теорема: в точках "склеивания" касательная к экстремали и касательная к граничной кривой должны совпадать.
Наконец, надо отметить, что экстремум может достигаться на "ломаных экстремалях", имеющих точки разрыва в первой или в старших производных. В этом случае в точках разрыва ti должны выполняться условия Вейерштрасса-Эрдмана:

Индекс ti-0 означает, что производные берутся при t, стремящемся к ti слева, а ti+0 означает, что t стремится к ti справа. Условия Вейерштрасса-Эрдмана являются теми добавочными условиями, которые позволяют нам найти угол наклона касательных к искомой функции у (t) в точках излома и тем самым полностью определить ее.
Экстремум может достигаться на разрывных функциях и на функциях, удовлетворяющим неравенствам
 (5.7)
(5.7)
Нахождение экстремалей в этом случае методами вариационного исчисления чрезвычайно сложно и часто невозможно. Для решения подобных задач эффективен принцип максимума Понтрягина (см. тему 5.8).
Вопросы и задания
1. Приведите и поясните особенности задач на поиск оптимальных решений.
2. Что такое функционал и в чем его отличие от классической функции?
3. Что такое экстремаль и как её найти в простейшем случае?
4. Поясните решение задачи нахождения линии кратчайшей длины, соединяющей две точки на плоскости.
5. Приведите формулировку и метод решения вариационной задачи, зависящей от нескольких функций.
6. Приведите формулировку и метод решения вариационной задачи, на решение которой наложены ограничения в виде алгебраических и интегральных равенств.
7. Приведите формулировку и метод решения вариационной задачи, решение которой склеиваются от отдельных линий.
8. Приведите формулировку и метод решения вариационной задачи, на решение которой наложены ограничения в виде алгебраических и интегральных неравенств.
5.2. Оптимальное управление ДПТ с независимым
возбуждением при постоянном моменте сопротивления
Функционалом является угол поворота α ротора ДПТ за заданное время Т
 (5.8)
(5.8)
Уравнением связи является уравнение динамики электропривода, записанное в относительных единицах,
 (5.9)
(5.9)
Ограничением является заданное количество тепла, выделившееся в обмотке якоря за время Т,
 (5.10)
(5.10)
Расширенная функция
 (5.11)
(5.11)
Уравнение Эйлера (по переменной ω) от расширенной функции и его решение
 (5.12)
(5.12)
Из последнего уравнения ряда (5.12) следует оптимальный закон изменения частоты вращения
 (5.13)
(5.13)
Подстановка (5.13) в уравнение (5.9) и вычисления позволяют найти оптимальный закон изменения тока
 (5.14)
(5.14)
Проведенные расчеты показали, что при оптимальном управлении частота вращения должна изменяться по параболическому закону (5.13), а ток – по линейному (5.14).
Постоянные интегрирования С1, С2 и коэффициент λ 0 определяются с учетом граничных условий ω 0 и ωТ для частоты вращения и заданных тепловыделений QЗ.
Примем условие, что в начале и конце движения ДПТ неподвижен: ω 0= ωТ =0. Тогда из (5.13) следуют:
 (5.15)
(5.15)
После подстановки (5.15) в (5.13) и (5.14) оптимальные законы примут вид
 (5.16)
(5.16)
Ток iОПТ в начале движения (при t=0) должен превышать момент нагрузки М. Тогда из (5.16) следует: λ0<0.
Для определения коэффициента λ 0 при М=0 вычислим интеграл (5.10):

 ,
,
откуда находим

Окончательно оптимальные законы изменения частоты вращения и тока якоря примут вид
 (5.17)
(5.17)
Графики сигналов ωОПТ при iОПТ оптимальном управлении приведены на рис.5.2.

Традиционно применяют разгон и торможение при постоянном токе якоря ДПТ (рис.5.3). За время Т при заданном значении QЗ поворот α вала составляет

всего лишь 75% от поворота при оптимальном управлении. Если же сравнивать оптимальное и традиционное управление ДПТ при условии, что в обоих случаях за время Т вал повернется на одинаковый угол α, то тепловыделения при традиционном управлении превысят тепловыделения при оптимальном управлении на 33%.
Близкое к оптимальному является управление по трапециидальной диаграмме частоты вращения ω (рис.5.4). Различие в угле поворота α составляет всего 12%.
С увеличением момента М сопротивления нагрузки различия в значениях α и Q становятся всё меньшими.
Вопросы и задания
1. Сформулируйте постановку задачи оптимального управления ДПТ при МС=const: определите функционал и ограничения.
2. Как ищется решение задачи оптимального управления ДПТ?
3. Как определяются постоянные величины, входящие в решение?
4. Какая эффективность оптимального управления в сравнении с традиционными управлениями ДПТ?
5.3. Оптимальное управление ДПТ с независимым возбуждением при ограничениях на частоту вращения и ток якоря
Ограничения на частоту вращения и ток якоря должны учитываться для любого электродвигателя.
1. Ограничение на частоту вращения.
К функционалу вида (5.8), уравнению связи вида (5.9) и ограничению вида (5.10) добавляется еще одно ограничение
 (5.18)
(5.18)
Вначале вариационным методом ищется решение, которое будет иметь вид (5.13), а после определения постоянных интегрирования С1 и С2 - вид (5.17). Далее строится график ωОПТ и на нем определяется максимальное значение ω. Если неравенство (5.18) не нарушается, то поставленную задачу можно считать решенной. График ωОПТ будет таким же, каким он изображен на рис.5.2.
Если неравенство (5.18) нарушается, то оптимальный закон изменения частоты вращения ω будет состоять и участков экстремалей вида (5.13) и граничных участков с предельной частотой ω=ωmax. В точках склеивания экстремалей и граничных участков должны выполняться условия Вейерштрасса-Эрдмана: значения производных к склеиваемым линиям в точках склеивания должны совпадать. Так как для участков с ω=ωmax производная  , то в точках склеивания производные для линий типа (5.13) должны быть равны нулю. Экстремали (5.13) являются параболами (рис.5.2) и точка, в которой
, то в точках склеивания производные для линий типа (5.13) должны быть равны нулю. Экстремали (5.13) являются параболами (рис.5.2) и точка, в которой  , совпадает с вершиной параболы. График ωОПТ будет иметь вид, показанный на рис.5.5, на котором параболические и линейный участки склеены в вершинах парабол. Там же показан график оптимального закона изменения тока якоря iОПТ, который на интервалах времени 0,5·Те, на которых график ωОПТ является графиком экстремалей, изменяется по закону (5.14), на интервалах времени, в которых ωОПТ=ωmax, ток якоря постоянный, причем в соответствии с уравнением связи (5.9) величина этого тока равна моменту нагрузки М.
, совпадает с вершиной параболы. График ωОПТ будет иметь вид, показанный на рис.5.5, на котором параболические и линейный участки склеены в вершинах парабол. Там же показан график оптимального закона изменения тока якоря iОПТ, который на интервалах времени 0,5·Те, на которых график ωОПТ является графиком экстремалей, изменяется по закону (5.14), на интервалах времени, в которых ωОПТ=ωmax, ток якоря постоянный, причем в соответствии с уравнением связи (5.9) величина этого тока равна моменту нагрузки М.

График 1-й экстремали (при t=0...0,5Te) и график тока описываются подобно (5.16) выражениями

График 2-й экстремали (при t=Т...Т-0,5Te) сдвинут вправо относительно первой на время Т-Те (на рис.5.5 показан такой величины сдвиг вершин парабол) и, поэтому, описание 2-й экстремали получается заменой t на t- (T-Te) =t-T+Te в описании 1-й экстремали. Такую же замену нужно сделать и в выражении тока.

Из выражения ωОПТ при значении t=0,5Te, определяем максимальное значение частоты вращения ωmax

Количество выделившегося тепла, которое должно быть равно заданному QЗ, определяется выражением

Из системы двух уравнений

определяются значения λ0 и Те и этим полностью решается задача расчета параметров графика ωОПТ, составленного из кусков экстремалей и граничного участка с ω=ωmax (рис.5.5).
2. Ограничение на ток якоря
К функционалу вида (5.8), уравнению связи вида (5.9) и ограничению вида (5.10) добавляется еще одно ограничение
 (5.19)
(5.19)
Вначале вариационным методом ищется решение, которое будет иметь вид (5.13), а после определения постоянных интегрирования С1 и С2 - вид (5.17). Далее строится графики ωОПТ и iОПТ. На графике iОПТ определяется максимальное значение. Если неравенство (5.19) не нарушается, то поставленную задачу можно считать решенной. Графики ωОПТ и iОПТ будут такими же, какими изображены на рис.5.2.
Если неравенство (5.19) нарушается, то оптимальный закон изменения частоты вращения ω будет содержать участки с линейно изменяющейся частотой вращения, так как при i=±iтах и М=const согласно (5.9) переменная ω изменяется с постоянной скоростью. На интервалах времени, где ограничение (5.19) не нарушается, график ωОПТ будет состоять из экстремали вида (5.13). В точках склеивания экстремалей и граничных участков с  должны выполняться условия Вейерштрасса-Эрдмана: значения производных к линиям в точках склеивания должны совпадать.
должны выполняться условия Вейерштрасса-Эрдмана: значения производных к линиям в точках склеивания должны совпадать.
График ωОПТ будет иметь вид, показанный на рис.5.6.

Основная сложность расчетов графика ωОПТ состоит в определении длительностей периода разгона ТР двигателя при постоянном токе i=+iтах и периода торможения ТТ при постоянном токе i=-iтах.
Вопросы и задания
1. Каким будет решение, если не нарушены ограничения на величину тока якоря и на максимальную частоту вращения?
2. Каким будет решение, если не нарушены ограничения на величину тока якоря, а частота вращения могла бы превысить максимальную?
3. Каким будет решение, если не нарушены ограничения на максимальную частоту вращения, тока якоря мог бы превысить максимальное значение?
5.4. Оптимальное управление ДПТ с независимым возбуждением при моменте сопротивления, зависящем от частоты вращения и времени
1. Момент сопротивления зависит от частоты вращения
Примером электропривода, момент сопротивления которого зависит от частоты вращения, является электропривод траловой лебедки. Сила натяжения ваеров пропорциональна скорости v выборки трала (F=F0+kv1,5) и, следовательно, момент сопротивления на валу двигателя пропорционален его частоте вращения (M=M0+kω1,5).
Ставится задача нахождения оптимального графика ωОПТ частоты вращения ω, доставляющего максимум функционалу (5.8) при ограничении (5.10) и уравнении связи (5.9), в котором М зависит от ω.
Уравнение Эйлера (по переменной ω) от расширенной функции (5.11) и его решение:

Умножим обе части последнего уравнения на  и выполним преобразования:
и выполним преобразования:

Получен универсальный результат
 ,
,
который связывает момент М и частоту вращения ω ДПТ при любой функциональной зависимости между ними, а не только той, которая существует для электропривода траловой лебедки.
В частности, для электропривода траловой лебедки оптимальный закон изменения частоты вращения ω при M=M0+kω1,5 удовлетворяет следующему дифференциальному уравнению

Решением этого дифференциального уравнения является график ωОПТ.
Оптимальный график тока якоря двигателя имеет вид

2. Момент сопротивления зависит от времени
Примером электропривода, момент сопротивления которого зависит от времени, является электропривод якорно-швартовного устройства. Для этого электропривода момент сопротивления уменьшается по линейной зависимости от времени M=M0+kt выборки цепи якоря.
Ставится задача нахождения оптимального графика ωОПТ частоты вращения ω, доставляющего максимум функционалу (5.8) при ограничении (5.10) и уравнении связи (5.9), в котором М зависит от t.
Уравнение Эйлера (по переменной ω) от расширенной функции (5.11) и его решение:

При моменте сопротивления, линейно изменяющемся во времени M=M0+kt, дифференциальное уравнение оптимального управления имеет вид
 ,
,
решением которого является параболическая функция
 (5.20)
(5.20)
С учетом уравнения связи 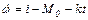 оптимальный график для тока якоря является линейным
оптимальный график для тока якоря является линейным
 (5.21)
(5.21)
В целом оптимальное управление получилось по форме таким же, как и для электропривода с постоянным моментом сопротивления - выражения (5.20) и (5.21) подобны выражениям (5.13) и (5.14).
Вопросы и задания
1. Какой является экстремаль в решении задачи оптимального управления ДПТ с моментом сопротивления нагрузки зависящем от частоты?
2. Какое управление ДПТ электропривода траловой лебедки в режиме выборки трала является оптимальным?
3. Какое управление ДПТ электропривода якорно-швартовного устройства в режиме подъема якоря является оптимальным?
5.5. Оптимальное управление ДПТ с независимым
возбуждением при моменте сопротивления,
зависящем от угла поворота вала
 Примером электропривода, момент сопротивления которого зависит от угла поворота вала, является электропривод руля. График механической характеристики руля имеет в первом приближении вид, изображенный на рис.5.7.
Примером электропривода, момент сопротивления которого зависит от угла поворота вала, является электропривод руля. График механической характеристики руля имеет в первом приближении вид, изображенный на рис.5.7.
Функционалом является время Т поворота руля на заданный угол αЗР
 (52.1)
(52.1)
Уравнением связи является уравнение динамики электропривода
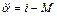 (5.22)
(5.22)
Ограничениями являются заданное количество тепла, выделившееся в обмотке якоря за время Т,
 (5.23)
(5.23)
и заданный угол поворота вала двигателя, который пропорционален заданному углу поворота руля αЗР,

Расширенная функция
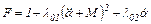
Уравнение Эйлера-Пуассона (по переменной α) от расширенной функции и его решение
 (5.24)
(5.24)
Механическая характеристика руля, приведенная на рис.5.7, описывается выражением
 (5.25)
(5.25)
После подстановки (5.25) в последнее уравнение цепи (5.24) получим дифференциальное уравнение для определения оптимального графика тока якоря двигателя
 (5.26)
(5.26)
Решение уравнения (5.26) имеет вид
 (5.27)
(5.27)
Оптимальный график для угла поворота αОПТ согласно (5.22) с учетом (5.25) и (5.27) определяется из следующего дифференциального уравнения
 (5.28)
(5.28)
Ищем решение последнего дифференциального уравнения цепи (5.28) как сумму свободного αСВ и принужденного αПР решений.
Свободное решение, найденное с учетом характеристического уравнения дифференциального уравнения (5.28), имеет вид

Принужденное решение, учитывающее вид правой части дифференциального уравнения (5.28), будет следующим
 (5.29)
(5.29)
Для определения коэффициентов В1 и В2 подставим (5.29) в (5.28)
 (5.30)
(5.30)
После преобразований, выполненных над (5.30), получено

Полное решение дифференциального уравнения (5.28) имеет вид

Для определения четырех постоянных интегрирования С1...С4 и времени Т нужно составить систему из пяти уравнений:
- два уравнения из граничных условий для угла α:

- два уравнения из условий неподвижности руля в начале и конце движения:

- одно уравнение как результат вычисления интеграла (5.23):
Поиск по сайту: