Критерий устойчивости Гурвица 5 страница

(3.7)

Период автоколебаний согласно (3.5) с учетом (3.6) и (3.7) равен

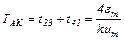
Расчет закончен.

Налицо громоздкость вычислений методом припасовывания. Более простое решение этой же задачи методом фазовых траекторий будет приведено в теме 3.5.

Вопросы и задания

1. На примере приведенных на рис.3.1 нелинейностей поясните, почему эти нелинейности нельзя линеаризовать?

2. В чем суть метода припасовывания, применяемого для расчета нелинейных САУ?

3. Дайте определение автоколебаниям и как определяются их амплитуда и период в приведенном расчете?

3.2. Определение и свойства фазовых траекторий.

Фазовые траектории линейных САУ 2-го порядка

Определение фазовых траекторий.

Метод фазовых траекторий является основным методом расчета нелинейных САУ. Основными достоинствами метода являются понижение порядка решаемых дифференциальных уравнений и наглядность решений.

Пусть САУ описывается дифференциальным уравнением вида

(3.8)

Фазовые переменные у₀, у₁, у₂,… этого дифференциального уравнения определяется как базовый сигнал у и производные от него:

В расчетах обычно используются две у₀, у₁ или три у₀, у₁, у₂ фазовые переменные. При двух фазовых переменных у₀ и у₁ порядок дифференциального уравнения (3.8) понижается на единицу, а решение уравнения в фазовых переменных отображается в виде фазовой траектории на плоскости с координатами у₀ и у₁ по осям абсцисс и ординат. При трех фазовых переменных у₀ , у₁ и у₂ порядок дифференциального уравнения (3.8) понижается на два, а решение уравнения в фазовых переменных отображается в виде фазовой траектории в трехмерном пространстве с координатными у₀ , у₁ и у₂. Понижение порядка дифференциального уравнения даже на единицу упрощает его решение и, как будет установлено ниже на примерах расчета, решения являются алгебраическими функциями, а не экспонентами и тригонометрическими функциями.

Свойства фазовых траекторий.

Ниже будем рассматривать приемы расчета нелинейных САУ в двух фазовых переменных у₀ и у₁ или у и . Фазовые траектории на плоскости у и обладают следующими свойствами (рис.3.4):

- в верхней полуплоскости движение по фазовым траекториям 1 осуществляется слева направо (так как в верхней полуплоскости и, поэтому значение у только возрастает), а в нижней – справа налево по траекториям 2;

- ось абсцисс у пересекается фазовыми траекториями 3 и 4 под прямым углом, так как на этой оси и, поэтому у не изменяется;

- линии отдельных траекторий 1 и 5 допускают разрывы по вертикали, если фазовое уравнение является алгебраическим, и разрывы не допускаются (линии 1 и 6), если фазовое уравнение дифференциальное любого порядка.

Фазовые траектории линейных САУ 2-го порядка.

Целью настоящего вопроса является установление на примере линейной САУ 2-го порядка соответствий между фазовыми траекториями и переходными процессами с присвоением названий фазовым траекториям и их особым точкам. Такие же соответствия существуют, в принципе, и в нелинейных САУ, что будет подтверждено соответствующими расчетами.

Пусть дифференциальное уравнение линейной САУ 2-го порядка имеет вид

Очевидно, что для этой САУ принужденное решение у_пр будет нулевым. От вида корней характеристического уравнения будет зависеть не только вид свободного решения, но и устойчивость САУ, т.е. придет ли система к принужденному значению.

Рассмотрим переходные процессы и фазовые траектории линейной САУ при различных корнях характеристического уравнения.

1. Корни чисто мнимые р_1,2=±jω.

Переходным процессом являются незатухающие гармонические колебания (рис.3.5а)

(3.9)

Производная от у (функция веса) равна

Составим из (3.9) и производной выражение

(3.10)

Последнее выражение является фазовой траекторией, так как в него входят только фазовые переменные у и . Фазовой траекторией является эллипс, а ее особой точкой является центр (рис.3.5б).

Рис.3.5 иллюстрирует тот факт, что замкнутой эллиптической фазовой траектории соответствует незатухающий гармонический переходный процесс в линейной САУ. Аналогичные замкнутые фазовые траектории имеются в нелинейных САУ с той разницей, что фазовая траектория не является эллипсом, а, поэтому, незатухающие переходные процессы являются негармоническими.

Незатухающие негармонические колебания в нелинейных САУ называются автоколебаниями.

2. Корни комплексные р_1,2=α±jβ.

Переходным процессом являются затухающие гармонические колебания (рис.3.6а) при α<0 и расходящиеся колебания (рис.3.6б) при α>0. Фазовыми траекториями являются, соответственно, сходящиеся и расходящиеся спирали, навивающиеся вокруг особых точек – фокусов.

3. Корни действительные р₁=α₁ и р₂=α₂ одинакового знака.

Переходным процессом являются затухающие экспоненциальные графики (рис.3.7а) при α_1,2<0 и расходящиеся экспоненциальные графики (рис.3.7б) при α_1,2>0. Фазовыми траекториями являются, соответственно, сходящиеся и расходящиеся пучки, привязанные к особым точкам – узлам.

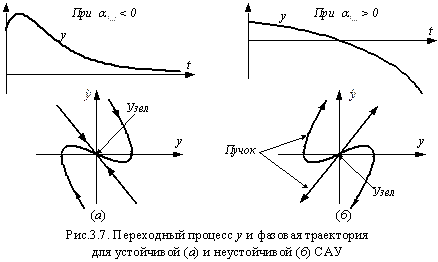
4. Корни действительные р₁=α₁ и р₂=α₂ разного знака.

Переходным процессом являются расходящиеся экспоненциальные графики (рис.3.8а). Фазовыми траекториями являются серии расходящихся линий, которые по форме подобны седлу (рис.3.8б).

В нелинейных САУ встречаются графики фазовых траекторий подобные всем здесь рассчитанным для линейных САУ и им соответствуют те же по форме графики переходных процессов.

Если построены графики фазовых траекторий и известны аналитические зависимости (формулы) 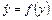для этих графиков, то по ним можно рассчитать переходный процесс по формуле

(3.11)

Вывод этой формулы такой:

откуда и .

Вопросы и задания

1. Дайте определение фазовым переменным и фазовым траекториям. Какие преимущества в расчетах САУ даёт переход к фазовым переменным и траекториям?

2. Какое существует соответствие между графиками переходных процессов и фазовыми траекториями для САУ, характеристическое уравнение которых имеет мнимые корни? Дайте определение автоколебаниям.

3. Какое существует соответствие между графиками переходных процессов и фазовыми траекториями для САУ, характеристическое уравнение которых имеет комплексные корни?

4. Какое существует соответствие между графиками переходных процессов и фазовыми траекториями для САУ, характеристическое уравнение которых имеет действительные корни одинаковых знаков?

5. Какое существует соответствие между графиками переходных процессов и фазовыми траекториями для САУ, характеристическое уравнение которых имеет действительные корни разных знаков?

3.3. Расчет фазовым методом нелинейной САУ

2-го порядка с идеальным трехпозиционным реле

Структурная схема САУ приведена на рис.3.9.

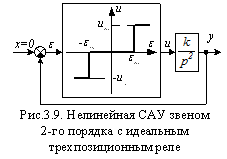Целью расчета является построение фазовой траектории для рассматриваемой САУ и на ее основе выработка заключения о характере переходного процесса в САУ.

Расчет выполняется в следующей последовательности:

1. Описываем САУ системой обыкновенных уравнений:

- дифференциальное уравнение линейного звена;

u=f (ε) - обобщенное описание нелинейности; (3.12)

ε=0-у - уравнение элемента сравнения.

Система (3.12) из трех уравнений содержит три сигнала-функции - сигнала-функции у, ε и и Нужно рассчитать выходной сигнал схемы – сигнал у, исключив из системы (3.12) сигналы ε и и. Однако, так как входным и выходным сигналами нелинейности являются, соответственно, ε и и, то желательно эти сигналы не исключать из системы уравнений, иначе потребуется перестройка графика нелинейности для иных входных и выходных сигналов, что сделать непросто. Учитывая третье уравнение ε=-у системы (3.12), исключим сигнал у. Получим следующее описание САУ

(3.13)

2. Преобразуем дифференциальное уравнение системы (3.13) в фазовое дифференциальное уравнение, которое будет содержать только фазовые переменные ε и и не будет содержать время t. Выполним преобразования

и (3.14)

Система (3.13) обыкновенных уравнений после подстановки в нее (3.14) превратится в систему фазовых уравнений

(3.15)

Так как система фазовых уравнений содержит дифференциальное уравнение, то на фазовой траектории не должно быть разрывов и скачков по любой оси - ε и (см. рис.3.4).

3. Подготавливаем фазовую плоскость к построению фазовых траекторий путем выделения на ней областей, в которых значение выходного сигнала и описывается формулой. Так как выходной сигнал и нелинейности принимает всего три значения (-и_т, 0 и и_т ), то таких формул будет три – и_=-ит, и=0 и и=и_т. Поэтому, областей на фазовой плоскости будет также три.

Из графика нелинейности, приведенной на рис.3.9, видно, что при ε<-ε_m значение выходного сигнала нелинейности равно –и_т, при ε>ε_m значение выходного сигнала нелинейности равно и_т, а при -ε_т ≤ ε ≤ ε_т равно 0. Разбиение фазовой плоскости в соответствии с этими условиями на три области приведено на рис.3.10. Области отделены друг от друга линиями переключения ЛП1 и ЛП2, так как на этих линиях изменяются скачком (переключаются) значения сигнала и.

4. Задавшись начальными условиями ε₀ и , решаем дифференциальное уравнение системы по областям, очерченными линиями переключения ЛП1 и ЛП2.

а). Область с и=и_т. Дифференциальное фазовое уравнение согласно (3.15)

и его решение

Это парабола 0-1, симметричная относительно оси ε, с ветвями, направленными справа налево.

б). Область с и=0. Дифференциальное фазовое уравнение согласно (3.15)

и его решение

(3.16)

Это прямая линия 1-2, параллельная оси ε.

в). Область с и=-и_т. Дифференциальное фазовое уравнение согласно (3.15)

и его решение

Это парабола 2-3, симметричная относительно оси ε, с ветвями, направленными слева направо.

г). Область с и=0. Это прямая линия 3-4 (3.16), параллельная оси ε.

5. Заключение о характере переходного процесса в САУ.

На рис.3.10 обозначены косой чертой одинаковые по величине отрезки. Их равенство следует из свойства симметричности графиков парабол и параллельности к оси абсцисс линий (3.16). Значит, фазовая траектория будет замкнутой линией, а переходный процесс будет периодическим незатухающим. Замкнутая линия - не эллипс и, поэтому, в САУ установятся автоколебания.

Вопросы и задания

1. Составьте систему обыкновенных уравнений, описывающую рассмотренную нелинейную САУ.

2. Переведите систему обыкновенных уравнений в систему фазовых переменных. Почему из системы фазовых уравнений нежелательно исключать те переменные, которые являются входным и выходным сигналом нелинейного элемента?

3. Как с учетом графика нелинейности производится разбиение на области фазовой плоскости? Поясните смысл линий переключения.

4. Как рассчитываются и стыкуются между собой участки фазовой траектории?

5. Как установить замкнутость фазовой траектории?

3.4. Расчет фазовым методом нелинейной САУ

2-го порядка 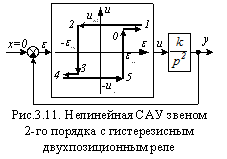с гистерезисным двухпозиционным реле

Структурная схема САУ приведена на рис.3.11.

Целью расчета является построение фазовой траектории для рассматриваемой САУ и на ее основе выработка заключения о характере переходного процесса в САУ.

Последовательность расчета та же, что описана в теме 3.3. Пункты 1 и 2 расчета те же, что в теме 3.3.

3. Подготавливаем фазовую плоскость к построению фазовых траекторий путем выделения на ней областей, в которых значение выходного сигнала и описывается одной формулой. Так как выходной сигнал и нелинейности принимает всего два значения (-и_т, и и_т ), то таких областей на фазовой плоскости будет две, в каждой из которых сигнал и неизменен.

Значение выходного сигнала u нелинейности равно и_т в следующих случаях (рис.3.11):

- если сигнал ε принадлежит участку 0-1-0 нелинейности (ε>ε_m) независимо направления движения по нему; на плоскости (рис.3.12) этому условию соответствует область, лежащая правее линии а-b-с;

- если сигнал ε принадлежит участку 0-2, на котором ε>-ε_m и одновременно движение по нему происходит справа налево, т.е. значение ε уменьшается (); на плоскости (рис.3.12) этому условию соответствует область, ограниченная ломанной линией с-b-d-e.

Объединение выделенных областей даёт область, расположенную правее ломанной линии a-b-d-e, в которой и=и_т. Левее этой линии расположена область, в которой и=-и_т. Линия a-b-d-e называется линией переключения ЛП, при пересечении которой фазовой траекторией скачком изменяется (переключается) знак сигнала и.

4. Задавшись начальными условиями ε₀ и , решаем дифференциальное уравнение системы по областям, очерченным линией переключения ЛП.

а). Область правее ЛП с и=и_т. Дифференциальное фазовое уравнение согласно (3.15)

и его решение

Это парабола 1-2, симметричная относительно оси ε, с ветвями, направленными справа налево.

б). Область левее ЛП с и=-и_т. Дифференциальное фазовое уравнение согласно (3.15)

и его решение

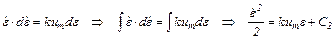
Это парабола 2-3, симметричная относительно оси ε, с ветвями, направленными слева направо.

5. Заключение о характере переходного процесса в САУ.

На рис.3.12 обозначены одинаковыми косыми чертами одинаковые по величине отрезки. Видно, что фазовая траектория является расходящейся спиралью (подобно рис.3.6б). САУ неустойчива.

Вопросы и задания

1. Поясните процедуру разбиения фазовой плоскости на области с постоянными значениями управляющего сигнала "и".

2. Обоснуйте спиральную форму фазовой траектории.

3.5. Расчет фазовым методом нелинейной САУ

1-го порядка с гистерезисным двухпозиционным реле

Структурная схема САУ приведена на рис.3.13.

Целью расчета является построение фазовой траектории для рассматриваемой САУ и на ее основе выработка заключения о характере переходного процесса в САУ.

1. Описываем САУ системой обыкновенных уравнений:

(3.17)

Система (3.17) из трех уравнений содержит три сигнала - сигнала-функции у, ε и и Нужно рассчитать выходной сигнал схемы – сигнал у, исключив из системы (3.17) сигналы ε и и. Однако, так как входным и выходным сигналами нелинейности являются, соответственно, ε и и, то желательно эти сигналы не исключать из системы уравнений, иначе потребуется перестройка графика нелинейности для иных входных и выходных сигналов, что сделать непросто. Учитывая третье уравнение ε=-у системы (3.17), исключим сигнал у. Получим следующее описание САУ

(3.18)

2. В систему (3.18) входят только фазовые переменные ε и и не входит как явная переменная время t. Значит система (3.18) является фазовой системой уравнений. Так как система фазовых уравнений содержит только алгебраические уравнения, то на фазовой траектории может быть разрыв (скачок) по оси (рис.3.4).

3. Этот пункт такой же, как пункт 3 в теме 31.

4. Задавшись начальными условиями ε₀ и (рис.3.14), строим линии фазовых траекторий по областям, очерченным линией переключения ЛП.

а). Область правее ЛП с и=и_т. Именно в этой области задана точка с начальными условиями ε₀ и . Алгебраическое фазовое уравнение согласно (3.18) имеет вид

Это прямая линия 1-2-3, проходящая через точку с координатами ε₁=ε₀ и , в которую САУ переходит скачком из точки 0 с начальными условиями ε₀ и . Линия 1-2-3 продлевается до ЛП, на которой ε=-ε_т.

б). Область левее ЛП с и=-и_т. Алгебраическое фазовое уравнение согласно (3.18) имеет вид

Это прямая линия 4-5, проходящая через точку с координатами ε₄=-ε_т и . Переход из точки 3 в точку 4 происходит скачком.

Линия 4-5 продлевается до ЛП, на которой ε=ε_т. Далее следует скачок в точку 2.

5. Заключение о характере переходного процесса в САУ.

Так как расчетом получена замкнутая фазовая траектория 2-3-4-5-2, то в САУ устанавливаются автоколебания. По данной циклической фазовой траектории легко рассчитать параметры автоколебаний – амплитуду А_АК и периода Т_АК. Амплитуда автоколебаний определяется непосредственно из рис.3.14

Период автоколебаний Т_АК равен сумме времен t_2-3 , t_3-4 , t_4-5 и t_5-2 движения по соответствующим участкам траектории 2-3-4-5-2. Учитываем, что движение на участках 3-4 и 5-2 происходит скачком и, поэтому, t_3-4 =0 и t_5-2=0. Ввиду симметрии участков 2-3 и 4-5 движение по ним требует одинакового времени, равного половине периода автоколебаний. Используя формулу (3.11) применительно к участку 4-5, рассчитываем полупериод автоколебаний

откуда

Такие же параметры А_АК и Т_АК автоколебания были рассчитаны в теме 3.1 методом припасовывания, но там расчет их был гораздо сложнее.

Вопросы и задания

1. Поясните процедуру вывода системы фазовых уравнений рассмотренной САУ.

2. Обоснуйте замкнутую форму фазовой траектории.

3. Как, используя фазовую траекторию, определить параметры автоколебаний?

3.6. Нелинейная САУ с переменной структурой

Наглядность решений, отображаемых на фазовой плоскости фазовыми траекториями дает уникальную возможность производить синтез нелинейных САУ с использованием графических возможностей фазового метода.

Рассмотрим линейную САУ 2-го порядка, изображенную на рис.3.13.

Передаточная функция замкнутой САУ имеет вид

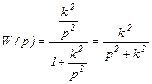
Корни характеристического уравнения чисто мнимые 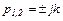. С такими корнями в САУ устанавливаются незатухающие гармонические колебания (см.рис.3.5), что является признаком того, что САУ находится на грани устойчивости. Фазовой траекторией является эллипс, причем размеры полуосей эллипса зависят от величины коэффициента k (см. (3.10)): при k>1 большей полуосью является полуось по (размер полуоси по в k раз больше полуоси по у) и эллипс вытянут по вертикали, а при k<1 эллипс вытянут по горизонтали.

Из разновытянутых по осям у и эллипсов можно составить фазовую траекторию, имеющую вид сходящейся спирали (рис.3.6а).

Обозначим малый коэффициент k П-регулятора (k<1) как k_М а большой (k>1) – как k_Б. Введем в САУ логическое устройство ЛУ (рис.3.16б), осуществляющее изменение величины коэффициента передачи k П-регулятора в зависимости от сигналов состояния у и (фазовых переменных) звена 2-го порядка, которое является объектом управления.

Разработаем такое ЛУ, которое изменяло бы коэффициент k П-регулятора в соответствии с рис.3.16а:

- при ЛУ должно замыкать верхний контакт в схеме, приведенной на рис.33.2б, устанавливая большой коэффициент k_Б П-регулятора;

- при - замыкать нижний контакт, устанавливая этим малый коэффициент k_М

Так как при проверке условий и не учитывается числовое значение произведения а учитывается только знак произведения , то в основу работы ЛУ может быть положена проверка только знака произведения . Устройство для проверки знака произведения проще устройства проверки знака произведения. Для проверки знака произведения можно использовать компараторы, работа которых описывается с точностью до постоянного множителя выражениям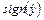и и (см.рис.1.1).

Структурная схема САУ с переменной структурой (СПС), в которой подробно раскрыто логическое устройство ЛУ, приведена на рис.3.17а. При одинаковых по знаку сигналах у и выходные напряжения е₁ и е₂ компараторов К1 и К2 будут одинаковыми по величине и знаку, поэтому к обмотке реле Р будет подведено нулевое напряжение и будет замкнут его НЗ-контакт в цепи с k_Б. При противоположных по знаку сигналах у и выходные напряжения е₁ и е₂ компараторов К1 и К2 будут одинаковыми по величине, но разными по знаку, поэтому к обмотке реле Р будет подведено максимально возможное напряжение и будет замкнут его НО-контакт в цепи с k_М.

Поиск по сайту: