Критерий устойчивости Гурвица 7 страница

Данный вид модуляции используется в схемах силовых цепей, например, в импульсных регуляторах постоянного напряжения (рис.4.2б). Методы расчета импульсных САУ с ШИМ-сигналами чрезвычайно сложные. На практике применяется следующий прием: расчеты в импульсных САУ выполняются на базе сигналов АИМ, а при выводе АИМ сигналы достаточно несложно преобразуются в ШИМ-сигналы (см. тему 4.2).

Частотно-импульсная модуляция – ЧИМ (упрощенно – ЧМ)

При ЧМ значение непрерывного (аналогового) сигнала x (t) преобразуется в частоту f_n следования импульсов (рис.4.3), где п – номер импульса. Амплитуда А импульсов и их длительность τ постоянные величины.

Сигналы с ЧИМ менее всего чувствительны к помехам. Методы расчета импульсных САУ с ЧМ-сигналами чрезвычайно сложные. На практике применяется следующий прием: расчеты в импульсных САУ выполняются на базе сигналов АИМ, а при выводе АИМ сигналы достаточно несложно преобразуются в ЧМ-сигналы.

По результатам рассмотрения различных видов импульсной модуляции непрерывных сигналов можно сделать тот вывод, что в расчетах импульсных САУ лучше всего использовать сигнал АИМ, а при учете ориентации на техническую реализацию импульсных САУ на базе микропроцессорной техники, использовать АИМ-сигнал с коэффициентом заполнения γ=1 (сигнал ступенчатой модуляции).

Рассмотрим особенности цифрового представления АИМ-сигналов в виде двоичных кодов. Цифровые двоичные коды изменяются дискретно и, поэтому, они в принципе не могут точно передать амплитуду импульса АИМ. Так, например, при разрядности кода, равной 4, число кодовых комбинаций составляет 2⁴=16, и при минимальном шаге изменения кода, равном единице младшего разряда кода, максимальная погрешность кодового представления составляет . Это довольно большая погрешность. Уменьшить погрешность можно путем увеличения разрядности кода. Например, при восьмиразрядном коде количество кодов равно 2⁸=256, а максимальная погрешность составляет .

Достоинства импульсных САУ на базе микропроцессоров:

1. Высокая точность обработки информации, так как обработка ведется по программе. Программа нечувствительна к дестабилизирующим факторам.

2. Возможна реализация алгоритмов обработки высокой сложности, что трудно реализуемо в САУ не импульсного типа.

3. Возможно управление одним микропроцессорным устройством большим числом (десятки-сотни) объектов, которое реализуется в режиме разделения времени, когда объекты обслуживаются микропроцессорным устройством последовательно и при большой тактовой частоте процессора создается иллюзия того, что все объекты будто бы обслуживаются одновременно.

Вопросы и задания

1. Какие САУ называются импульсными и цифровыми? Назовите основные достоинства импульсных САУ.

2. Поясните принцип амплитудно-импульсной модуляции и области применения АИМ в САУ.

3. Поясните принцип широтно-импульсной модуляции и области применения ШИМ в САУ.

4. Поясните принцип частотно-импульсной модуляции и области применения ЧИМ в САУ.

5. Поясните принцип цифровой модуляции их области её применения в САУ.

4.2. Схемы импульсных модуляторов

Рассмотрим схемы амплитудно-импульсных модуляторов и преобразователь АИМ сигнала в сигнал ШИМ.

Схемы амплитудно-импульсных модуляторов

1. Устройство выборки-хранения (УВХ) применяется только в импульсных, но не в цифровых САУ. Схема УВХ приведена на рис.4.4.

Ко входу ОУ, имеющем большое входное сопротивление (входной каскад ОУ выполнен на полевом транзисторе), подключен запоминающий конденсатор С_З. Конденсатор С_З периодически на малое время подключается к аналоговому сигналу и (t) через аналоговый ключ на полевом транзисторе VT и принимает значение и (пТ). Выходной сигнал ОУ, включенного по схеме повторителя в коэффициентом передачи равным 1. Выходной сигнал и_И (t) является ступенчатым, амплитуда которого равна и (пТ).

2. Устройство цифровой модуляции и демодуляции (рис.4.5).

Многовходовой АЦП по сигналам микропроцессора МП по очереди через период Т подключается к аналоговым сигналам u_i (t), преобразует их в цифровые коды К_ui. Об окончании преобразования очередного аналогового сигнала АЦП сообщает микропроцессору, который переписывает образовавшийся код в оперативное запоминающее устройство ОЗУ, и переводит АЦП в пассивный режим (преобразования в аналогового сигнала в нем останавливаются). Далее МП обрабатывает по программе цифровой код К_ui, превращая его в код выходного сигнала К_уi. По сигналу МП код К_уi преобразуется с помощью ЦАП в аналоговый сигнал у_i (t).

Все коды - К_ui и К_уi – будучи сформированными сохраняются неизменными в течение периода Т, минимальная величина которого определяется задержкой, вызванной работой программы микропроцессора.

Устройство преобразования АИМ сигнала в ШИМ сигнал

Необходимость преобразования амплитудно-модулированного сигнала в широтно-импульсный отмечена в теме 4.1. Принцип преобразования поясняется рис.4.6.

Пусть импульсы АИМ сигналов с амплитудами A_i действуют в течение времени Т – периода следования импульсов. Площадь, занимаемая импульсом, отмечена штриховкой под углом 45^о, и равна

Площадь, занимаемая ШИМ сигналом длительностью τ_i с постоянной амплитудой А, отмечена штриховкой под углом -45^о, и равна

Из условия равенства площадей S_i.АИМ и S_i.ШИМ получаем формулу пересчета амплитуды A_i АИМ сигнала в длительность τ_i ШИМ сигнала

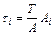(4.1)

Преобразование (4.1) может быть выполнено как на аналоговых, так и на цифровых устройствах. В последнем случае преобразование осуществляется по программе, которая по величине A_i формирует выходной импульс длительностью τ_i пропорциональной A_i (рис.4.7).

Вопросы и задания

1. Поясните принцип действия УВХ как амплитудно-импульсного модулятора.

2. Поясните принцип действия микропроцессорного амплитудно- импульсного модулятора.

3. Поясните принцип действия преобразователя АИМ-сигнала в ШИМ-сигнал.

4.3. Способы описания импульсных сигналов.

Особенности соответствия оригиналов и изображений

Сложность аналитического описания импульсных сигналов обусловлена следующими причинами:

1) импульсы являются дискретными сигналами и их число в выделенной в САУ линии связи не ограничено (бесконечное большое число);

2) каждый импульс из бесконечной их последовательности не описывается аналитически формулой.

При определенных допущениях обе проблемы разрешимы в рамках новых методов математического описания импульсных сигналов. Существуют 4 формы (способа) описания импульсных сигналов:

1) решетчатая функция (РФ);

2) импульсная функция (ИФ);

3) преобразование Лапласа от импульсной функции;

4) z -изображение от импульсной функции.

1. Решетчатая функция

Если x (t) – непрерывный сигнал, то решетчатой функцией называется множество значений непрерывного сигнала, определенных в дискретные моменты времени, совпадающие с моментами съема импульса амплитудно-импульсным модулятором

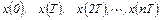
или – упрощенно, (4.2)

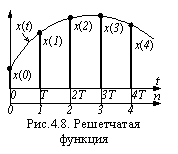
Графическим представлением РФ являются столбики, заканчивающиеся точкой (рис.4.8).

Достоинствами описания импульсов решетчатыми функциями являются:

1) РФ является действительной характеристикой (амплитудой) каждого импульса бесконечной их последовательности;

2) РФ входит во все другие формы описания импульсных сигналов.

Недостатками описания импульсов решетчатыми функциями являются:

1) РФ не является аналитическим (формульным) описанием импульсов, а представляет собой бесконечное множество элементов вида х (пТ) (4.2);

2) реализации (столбики) РФ не являются реализациями физического сигнала и, поэтому, невозможно рассчитать реакцию любого физического звена на импульсы РФ.

2. Импульсная функция ИФ

Составим произведение п -го импульса на δ -импульс, смещенный вправо на п тактов (рис.4.9а). Получим п -й импульс импульсной функции

,

который обладает следующими свойствами:

1) при t=nT импульс сигнала имеет бесконечно большую амплитуду, бесконечно малую длительность и площадь S (n) равную значению х (п);

2) при t≠nT значение равно нулю.

Определим импульсную функцию как сумму отдельных импульсов :

(4.3)

В выражении (4.3) время t изменяется непрерывно, а функция изменяется дискретно, принимая значениях в моменты t=nT, а остальное время – нулевое.

Графическим представлением ИФ являются бесконечно высокие столбики, заканчивающиеся стрелкой, у которых имеется волнистая вставка-вырезка, ограничивающая высоту столбиков (рис.4.9б).

Достоинствами описания импульсов импульсными функциями являются:

1) ИФ является формулой, объединяющей бесконечную последовательность импульсов математическим знаком суммирования;

2) ИФ содержит физические сигналы, на каждый из которых может быть рассчитана реакция физического звена – функция веса k (t)(см. тему 1.1).

Недостатками импульсной функции является:

1) аналитическое описание ИФ имеет формулу бесконечного суммирования, которую довольно сложно использовать в инженерных расчетах;

2) ИФ представляет собой физически нереализуемую функцию из-за ее бесконечной высоты отдельных импульсов.

3. Преобразование Лапласа от импульсной функции

Выполним вычисления преобразование Лапласа от ИФ:

(4.4)

Вычислим интеграл в квадратных скобках

(4.5)

Интеграл от бесконечной величины дал конечный результат. Это поясняется тем, что преобразование Лапласа основано на интегрировании (4.4) и им определяется площадь δ- функции, которая, по определению, равна единице.

Подставляем (4.5) в (4.4)

(4.6)

В последнее выражение входят только конечные величины, и в этом его преимущество перед ИФ, содержащей под знаком суммирования величины бесконечно больших значений.

Недостаток формулы (4.6) в том, что она является суммой бесконечного ряда и, поэтому, ее сложно использовать в инженерных расчетах.

4. z-изображение от импульсной функции

В выражении (4.6) выполним подстановку . Получим z -изображение от импульсной функции

(4.7)

Пока явственно видно, что запись z -изображение менее громоздка в сравнении с записью преобразованием Лапласа от импульсной функции .

Теперь развернем z -изображение (4.7) в ряд

(4.8)

Видно, что ряд представляет собой сумму произведений значений решетчатой функции х (п) на отрицательные степени символа z, причем значение отрицательного показателя степени совпадает с номером импульса,

С формальной точки зрения z -изображение представляют собой сумму членов геометрической прогрессии. Основание геометрической прогрессии, каким является символ , по модулю меньше единицы, так как именно положительном значении действительной части оператора р вычисляется преобразование Лапласа (4.4).Поэтому геометрический ряд (4.8) в принципе может сходиться, а прогрессия может быть свернута в конечную формулу.

Рассчитаем z -изображение от единичного скачка (рис.4.10). Для него значение решетчатой функции, взятое непосредственно из графика 1 (t), равно х (0) =1, х (1) =1, х (2) =1,…, х (п) =1. Подставляем эти значения РФ в выражение (4.8) и вычисляем сумму геометрической прогрессии

Выполненный расчет показал, что z -изображение от единичного скачка оказалось конечной формулой. В этой формуле в упакованном виде содержится информация о любом импульсе из бесконечной их последовательности. Для извлечения этой информации (распаковки z -изображения в конечной форме) необходимо произвести деление многочлена числителя на многочлен знаменателя:

Результатом деления является ряд

,

в котором коэффициенты при степенях символа z имеют значения 1. Они же, согласно (4.8) являются значениями решетчатой функции х (п). Так как для всех п≥0 значения х (п) =1, оригиналом данного изображения является единичный скачок, для которого 1 (t) =1 при t≥0.

Аналогично приведенному вычислению z -изображения от единичного скачка можно вычислить z -изображения от любых других сигналов. Для типовых сигналов САУ такие вычисления выполнены и приведены в табл.4.1.

Таблица 4.1

Основные формулы z -преобразования

Оригинал x (t)	Изображение х (р) по Лапласу	z -изображение x (z)
δ (t)	1	1
δ (t-nT)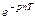
1(t)
Оригинал x (t)	Изображение х (р) по Лапласу	z -изображение x (z)
t

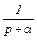
Особенности соответствия оригиналов и изображений

Принцип действия модуляторов состоит в том, что периодически с непрерывного сигнала x (t) снимается мгновенное значение и запоминается на период Т. В промежутке между съемами значений аналогового сигнала x (t) для импульсов сигнал x (t) может изменяться произвольным способом (рис.4.11) по графикам x₁ (t), x₂ (t), x₃ (t) и т.п. Эта особенность импульсных САУ закреплена в использовании решетчатой функции для описания импульсов (рис.4.8). Графики решетчатой функции визуально плохо воспринимаются. В условиях неопределенности действительного графика x (t) оригинала для лучшего восприятия решетчатой функции будем соединять ее вершины прямыми линиями, т.е. линиями графика x₂ (t).

Очевидно, что неопределенность в определении действительного графика x (t) будет уменьшаться с уменьшением периода Т следования импульсов. Если τ_min – минимальный период гармонической составляющей разложения в ряд Фурье функции x (t), то период Т следования импульсов, при котором возможно по значениям решетчатой функции однозначно восстановить график x (t), определяется неравенством Котельникова

Т ≤ 0,5∙τ_min

Вопросы и задания

1. Поясните способ описания импульсных сигналов решетчатыми функциями и назовите достоинства и недостатки способа.

2. Поясните способ описания импульсных сигналов импульсными функциями и назовите достоинства и недостатки способа.

3. Поясните способ описания импульсных сигналов изображениями их по Лапласу и назовите достоинства и недостатки способа.

4. 3. Поясните способ описания импульсных сигналов z-изображениями и назовите достоинства и недостатки способа.

5. Поясните свойства неооднозначности оригиналов и z-изображений импульсных сигналов и как эту неоднозначность свести к минимуму?

4.4. Дискретные передаточные функции звеньев

Пусть на вход непрерывной части с передаточной функцией W_НЧ(р) поступают импульсы x_И (t), сформированные амплитудно-импульсным модулятором АИМ из непрерывного сигнала x (t) (рис.4.12). Выходной сигнал у (t) непрерывной части является суммой реакций на отдельные импульсы x_И (t), поступившие на ее вход.

Для реализации возможности расчета с использованием z -изображений реакции непрерывной части на поступающие на её вход прямоугольные импульсы, перейдем к эквивалентной импульсной САУ, изображенной на рис.4.13.

Входной непрерывный сигнал x (t) преобразуется дельта-импульсным модулятором δ-ИМ в импульсную функцию x* (t). Сигналы x* (t) импульсной функции поступают на формирователь импульсов, являющийся линейным звеном с некоторой передаточной функцией W_ФИ (р), который импульсы x* (t) превращает в реальные прямоугольные импульсы x_И (t). На выходе непрерывной части с передаточной функцией W_НЧ (р) образуются действительный сигнал у (t). Установим на линии сигнала у (t) дельта-импульсный модулятор δ-ИМ, работающий с периодом Т синхронно с модулятором сигнала x (t). В результате модуляции будут получена импульсная функция у* (t). У этой импульсной функции площади отдельных импульсов будут равны значениям выходного сигнала у (t) в дискретные моменты времени.

Определим передаточную функцию W_ФИ (р) формирователя импульсов исходя из заданных сигналов на его входе и выходе (рис.4.14). Выходной единичный импульс 1_И (t) ФИ может быть заменен разностью дух единичных скачков 1 (t) и 1 (t-Т), которые сдвинуты относительно друг друга на период Т, т.е. 1_И (t) =1 (t) -1 (t-Т). Изображения по Лапласу входного и выходного сигналов имеют вид

Передаточная функция ФИ определим как

Два последовательно соединенных линейных звена на рис.4.13 заменяем одним звеном, называемым приведенной непрерывной частью, с передаточной функцией

Схема с рис.4.13 превратится в схему, приведенную на рис.4.15.

От входной х* (t) и выходной у* (t) импульсных функций существуют соответствующие z -изображения x (z) и y (z). Установим связь между импульсными функциями х* (t) и у* (t) с использованием рис.4.16.

Входной сигнал х* (t) представляет собой (см. (4.3)) сумму δ -импульсов, сдвинутых по оси времени на п тактов и имеющих площадь, равную х (п). Реакцией приведенной непрерывной части на каждый δ -импульс является функция веса k (t-nT), сдвинутая вправо на п тактов и умноженная на площадь входного импульса, которая равна х (п). На рис.4.16 показаны графики х (0) k (t), х (1) k (t-T), х (2) k (t-2T) как реакции приведенной непрерывной части на импульсы х*(0), х*(1),х*(2) входного сигнала х* (t). Суммой графиков х (0) k (t), х (1) k (t-T), х (2) k (t-2T),…. является выходной сигнал у (t). Дельта-импульсный модулятор из сигнала у (t) формирует импульсную функцию у* (t), состоящую из импульсов у* (0), у* (1), у* (2),….

Импульсная функция выходного сигнала у (t) по определению (см. (4.3)) равна

(4.9)

Выходной сигнал у (t) согласно рис.4.16 определяется выражением

(4.10)

Подставляем (4.10) в (4.9)

(4.11)

Применив к (4.11) преобразование Лапласа и затем, перейдя к z -изображению, получим

(4.12)

Выражение называется дискретной передаточной функцией (ДПФ) звена

(4.13)

Согласно (4.12) определение дискретной передаточной функции такое же, как и в линейной САУ, а именно, есть отношение изображений выходного и входного сигналов звена

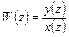(4.14)

Смысл дискретной передаточной функции заключается в том, что она связывает между собой решетчатые функции и, следовательно, амплитуды импульсов на входе и выходе звена. Если известна решетчатая функция x (z) входного сигнала, то с использованием дискретной передаточной функции W (z) можно рассчитать решетчатую у (z) функцию выходного сигнала звена. Результат (4.14) свидетельствует, что импульсные САУ в отношении решетчатых функций или амплитуд импульсов являются линейными САУ.

ДПФ можно вычислить либо по формуле (4.13), либо по более удобной в расчетах формуле

, (4.15)

где – символ, указывающий на операцию перехода от изображения по Лапласу к z -изображению.

Поиск по сайту: