Определения. 1) попарно независимы ó - независимы при

Рассмотрим события

1) попарно независимы ó - независимы при

2) независимы в совокупности или взаимно независимы ó если k n и

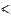
1 n () =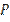

Заметим, что понятие 2 более сложное, чем 1. И из 2 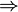1, обратное неверно.

Пример, когда из 1 не следует 2 (пример Бернштейна):

Имеется правильный тетраэдр, все грани которого - правильные треугольники, раскрашенные в один из четырех цветов – Белый, Красный, Синий, Пестрый (БКС).

Нас будет интересовать грань, которая окажется внизу, и одно из трех событий – Б,К,С. (Б – на нижней грани присутствует белый цвет и так далее.)

=

Будут ли они попарно независимы?

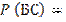
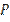= = (Б)

А теперь для независимости в совокупности:

= (Б)

Вывод: понятия попарной независимости и независимости в совокупности различны.

Независимость - алгебр

Пусть имеется () – вероятностное пространство.

Пусть ₁ - - алгебра событий , - алгебра

₂ - - алгебра событий

₁ и ₂ – независимые - алгебры, если и ₂ события являются независимыми.

Пример:

1) Невозможное событие независимо с любым другим событием.

2) Достоверное событие независимо с любым другим событием.

3) Вероятность Р - площадь кусочка

Рассмотрим – алгебру измеримых по Лебегу подмножеств прямой.

_1-- - алгебра на оси ОХ;

₂ - - алгебра на оси ОУ;

Тогда

₁={ | ₁ } и

₂={ ₂ } независимые – алгебры.

Лекция 3 (21.09.10)

Поиск по сайту: