АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Предельные теоремы в схеме Бернулли

Читайте также:
  1. В схеме, состоящей из конденсатора и катушки, происходят свободные электромагнитные колебания. Энергия конденсатора в произвольный момент времени t определяется выражением
  2. Вектор электрического смещения ( электрической индукции) D. Обобщение теоремы Гаусса для вещества.
  3. Виды средних издержек. Эффект отдачи от масштаба производства в положительных и отрицательных действиях и динамика средних издержек. Предельные издержки.
  4. Доказательство (теоремы).
  5. Долгосрочные предельные и средние затраты
  6. Запредельные формы психического напряжения
  7. Издержки производства в краткосрочном периоде. Постоянные и переменные издержки. Общие и средние издержки. Предельные издержки.
  8. Используя теоремы сложения и умножения, а также формулы комбинаторики
  9. Испытания Бернулли. Формула Бернулли.
  10. Нарушение контакта в электрической схеме прибора.
  11. Общие теоремы строительной механики
  12. Определения и теоремы

По-прежнему рассматриваем испытаний Бернулли. И нас по-прежнему интересует величина . Вы скажете, а зачем нам что-то искать, есть же: . Хорошо, а что делать в случае 10000-кратного подбрасывания монеты? Например . Большое это число или маленькое?

Каков же ответ? Будем вычислять с некоторой погрешностью.

Рассмотрим испытаний Бернулли, , 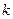-число успехов в испытаниях.

Локальная теорема Муавра-Лапласа. Справедливо следующее соотношение

равномерно по k: при фиксированном . Это означает, что

, где

-функция Гаусса.

Для функции существуют таблицы, которые показывают значения функции в различных точках. Таблицы устроены следующим образом:

X     …    
0,0          
0,1          
…          
1,4        
…          

Доказательство (теоремы):

Будем пользоваться следующими утверждениями, известными из курса математического анализа:

Лемма 1 (Формула Стирлинга).

Лемма 2. где для всех

Имеем

,

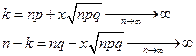
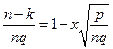
Запишем, что такое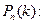

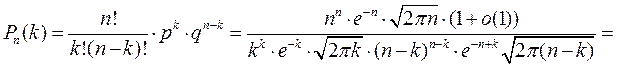
Рассмотрим

Итак, .

Перепишем . Теорема доказана.

 

 

Лекция 4. (28.09.10)

Задача: Пусть есть 2 числа и : 0 n.

Как вычислить

Возникают сложности: 1) в степенях, 2) в количестве слагаемых.

Можно заменить на приближение (по локальной теореме), но тогда погрешность может быть очень большой!

Ответ дается в следующей теореме.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)