АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема (Интегральная теорема Муавра - Лапласа)

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Внешние эффекты (экстерналии). Теорема Коуза.
  3. Внешние эффекты трансакционные издержки. Теорема Коуза
  4. Внешние эффекты, их виды и последствия. Теорема Коуза
  5. Внешние эффекты. Теорема Коуза.
  6. Вопрос 1 теорема сложения вероятностей
  7. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  8. Вопрос. Теорема Котельникова (Найквиста)
  9. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  10. Гранична теорема Пуассона
  11. Дискретизація сигналу – теорема відліків (Котельникова)
  12. Друга теорема економіки добробуту та її значення

Справедливо равенство:

Здесь k – число успехов, n – число испытаний.

Следствие из теоремы:

Доказательство этой теоремы последует в курсе позже, как частный случай более общей теоремы.

Как применять теорему? Если n очень большое, то

Обозначим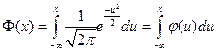

Свойства функции :

1) 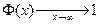и ;

2) строго возрастает;

3) ;

4) ;

 

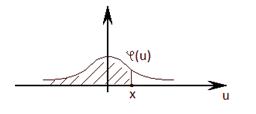
Существуют таблицы для :

X     …    
0,0          
0,1          
0,2          
…          
1,2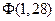        
…          

 

 

Рассмотрим новую задачу.

Пусть N=n, k - фикс. Вопрос: как при больших n найти вероятность получения ровно k успехов, если p мало? В этом случае локальная теорема Муавра-Лапласа дает слишком большую погрешность.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)