АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Закон больших чисел

Читайте также:
  1. B) Наличное бытие закона
  2. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  3. II закон Кирхгофа
  4. II. Законодательные акты Украины
  5. II. Законодательство об охране труда
  6. II.3. Закон как категория публичного права
  7. III. Государственный надзор и контроль за соблюдением законодательства об охране труда
  8. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  9. IX.3.Закономерности развития науки.
  10. А 55. ЗАКОНОМІРНОСТІ ДІЇ КОЛОГИЧЕСКИХ ФАКТОРІВ НА ЖИВІ ОРГАНІЗМИ
  11. А) Закон диалектического синтеза
  12. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.

Определение. Пусть - последовательность случайных величин,

Закон больших чисел (ЗБЧ) для последовательности

( или

)

Замечание. ЗБЧ для ЗБЧ для

Определение. Говорят, что для последовательности выполнен усиленный ЗБЧ (УЗБЧ), если

почти наверное.

 

А для каких последовательностей случайных величин выполняется ЗБЧ?

На этот вопрос отвечают следующие теоремы, в которых даны только лишь достаточные условия.

Теорема. (ЗБЧ Маркова)

- случайные величины.

Существуют и Тогда выполнен ЗБЧ.

Доказательство.

Теорема. (ЗБЧ Чебышева)

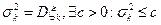
- попарно независимые случайные величины. Тогда выполнен ЗБЧ.

Доказательство.

Выполнены условия т. Маркова ЗБЧ.

Следствия. (из теоремы Чебышева)

1) Если - независимые одинаково распределенные случайные величины, выполнен ЗБЧ.

2) - независимые случайные величины.

Заметим, что следствие 2) является теоремой о ЗБЧ для испытаний Бернулли.

Теорема. (ЗБЧ Хинчина)

- независимые одинаково распределенные случайные величины,

Тогда выполнен ЗБЧ.

Доказательство этой теоремы будет представлено в нашем курсе позже.

 

 

Лекция 12 (23.11.10)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)