 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определения
I. Сходимость по вероятности
.
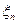
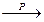
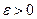
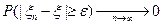II. Сходимость с вероятностью 1 или почти наверное
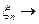
п. н. 
.
III. Сходимость в среднем порядка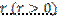 
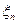
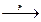
существуют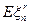 
и 
и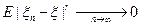 
.
IV. Сходимость по распределению
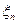
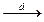
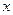- точки непрерывности 
.
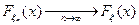Замечание: в пункте IV сходятся не случайные величины, а их функции распределения. При этом случайные величины могут быть далеки друг от друга.
Пример: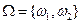 
, 
, 
; 
, 
.
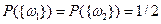
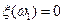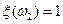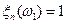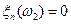
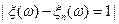и 
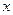
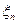
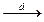
Теорема: (О соотношениях между видами сходимостей)
, 
, 
.
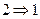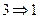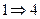Доказательство.
.
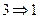
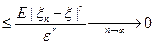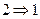
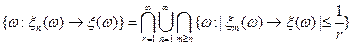
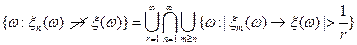
2 
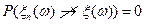
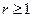
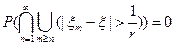
{Пусть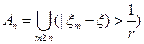 
, тогда 
( 
)}
.
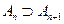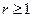
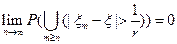Отметим, что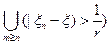 
= 
;
=
= 
.
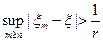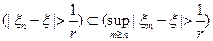
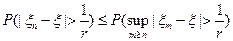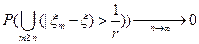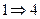
Пусть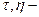 
случайные величины. Тогда всегда верно:
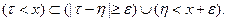
Тогда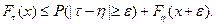 
Пусть 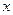- точка непрерывности функции распределения .
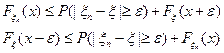
Устремим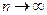 
и получим в 1) и 2) соотношениях:
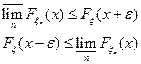
А теперь устремим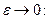 
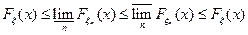
Поскольку верхний и нижний предел “зажаты” одним и тем же числом 
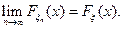
Поиск по сайту: