Определение. Функцией распределения случайной величины функцию :

Функцией распределения случайной величины функцию : .

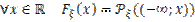Замечание.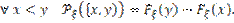

Покажем справедливость последнего равенства.

Имеем

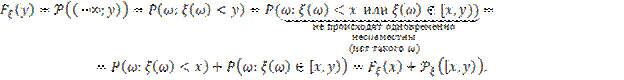
Таким образом, мы можем утверждать, что функция распределения и распределение однозначно определяют друг друга.

Свойства функции распределения.

1) 0 ;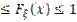

2)

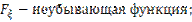
3)

4)

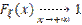
Доказательство.

1) = ;

2) Если , то = .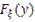

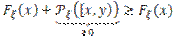3) Необходимо показать, что (*)

Пусть

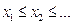и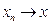

Рассмотрим 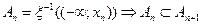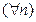- последовательность “расширяющихся событий” и .

По свойству вероятности .

Таким образом, (*) выполнено.

Замечание: Если бы мы определили функцию распределения равенством: , тогда свойство 3) необходимо заменить на непрерывность справа.

4) Рассмотрим событие ; ; .

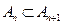
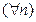По свойству вероятности .

Но .

Но это возможно только когда первое слагаемое равно 1, а второе равно 0.

Доказали для 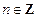. Пользуясь свойством 2) (монотонностью функции распределения) распространяем это свойство на все x.

Теорема: Пусть 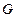: и удовлетворяет свойствам 2,3,4. Тогда 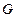- функция распределения некоторой случайной величины.

Доказательство: Пусть 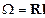, = 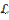, определим сначала 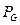на полуоткрытых интервалах равенством: 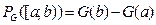. Затем естественным образом продлим на все измеримые подмножества прямой. Здесь 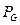- вероятностная мера (что легко проверяется).

Таким образом, определили вероятностное пространство: , .

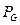
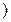Пусть 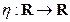; 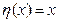- случайная величина.

Имеем 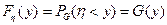, т.е. теорема доказана.

Задача: Задан конечный набор функций распределения: , числа 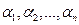: 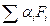- функция распределения?

Поиск по сайту: