Теорема (Неравенство Колмогорова)

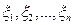- независимые случайные величины, у которых существуют мат. ожидания и дисперсия 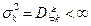. Рассмотрим 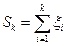. Тогда для любого справедливо неравенство:

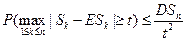
{Это обобщение неравенства Чебышева, так как всегда справедливо неравенство:

}

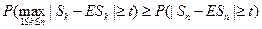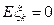
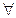
Замечание: Будем в дальнейшем считать, что . Это не умаляет общности рассуждений, т.к. мы рассматриваем центрированные случайные величины.

Доказательство: рассмотрим случайную величину 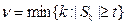или 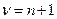, если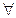 ; 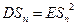(второй момент).

Рассмотрим следующие величины: – индикатор, 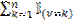– сумма индикаторов. Она равна либо 0, либо 1 (события при ).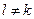

) = ;

= +

+ + .

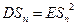
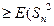
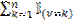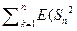
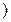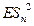
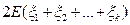
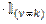
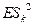
(Верно, поскольку 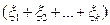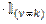и независимы и , а 0)

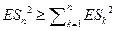
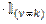
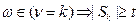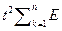
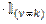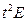
{Если } = = 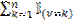{причем 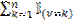= 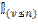} = 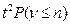{событие } =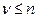

= .

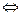
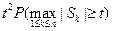Теорема (УЗБЧ):

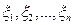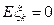
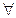
- независимые случайные величины, 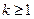, существует дисперсия 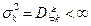и пусть . Тогда 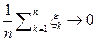почти наверное (п.н.).

Док-во. Пусть 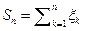, 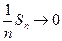п. н.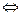

(*);

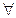
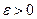
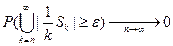
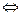
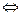
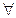
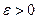
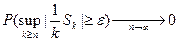Введем ;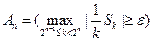

(*) (**)

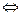
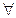
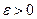
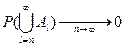Проверим, верно ли это: (*) (**)?

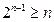
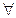
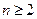
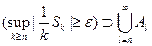
Следовательно, (*) (**).

(**) (*)?

Рассмотрим 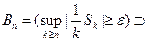(последовательность вложенных друг в друга событий).

В частности, если рассмотреть 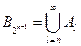- последовательность, поэтому,

(*)

Далее,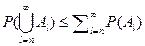

=

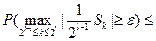
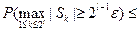
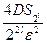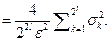Тогда

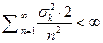
(**) выполнено.

Следствие. В ЗБЧ Чебышева 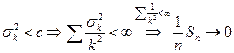п. н. , а это и есть ЗБЧ.

Поиск по сайту: