 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Свойства вероятности
Имеется произвольное вероятностное пространство ( )
)
Свойства:
1) P( ) =1 - P (A),
) =1 - P (A), 
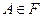
2) 0  P(A)
P(A)  1,
1, 
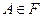
3) P( ) = 0
) = 0
4) P (A ∪ B) = P(A) + P(B) – P(AB)
4*)  ;
;
5)  ;
;
6)  («событие А предшествует событию В» или «событие А влечёт за собой событие В»)
(«событие А предшествует событию В» или «событие А влечёт за собой событие В») 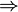

7) Пусть имеется последовательность расширяющихся событий 
8) Пусть имеется последовательность вложенных событий 
Свойства 7),8) принято называть свойствами непрерывности вероятности.
Доказательство:
1) A,  – несовместные события
– несовместные события  P(A
P(A  ) = P(A) + P(
) = P(A) + P( ); P(A
); P(A  ) = P (Ω) = 1
) = P (Ω) = 1 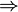 P(
P( ) = 1 – P(A).
) = 1 – P(A).
2)Левое неравенство – аксиома 1.
Правое: 1 = P(A) + P( ), P(
), P( )
) 
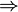 P(A) + P(
P(A) + P( )
)  P(A)
P(A)
3)  =
= 
 P(
P( ) = 1 - P (Ω) = 0
) = 1 - P (Ω) = 0
4) A ∪ B = A  ∪ AB ∪
∪ AB ∪  , где A
, где A  , AB,
, AB,  - попарно несовместные события
- попарно несовместные события
3 акс: P (A ∪ B) = P(A  ) + P(AB) + P (
) + P(AB) + P ( ) + P(AB) - P(AB), где P(A
) + P(AB) - P(AB), где P(A  ) + P(AB) = P(A),
) + P(AB) = P(A),
P ( ) + P(AB) = P(B).
) + P(AB) = P(B).
6) B = AB ∪  = A ∪
= A ∪  , где A и
, где A и  – несовместные.
– несовместные.
P (B) = P (A) + P ( )
)  P(A), т.к. P (
P(A), т.к. P ( )
)  0.
0.
5)  ,где
,где 

 ,
,  ,… и попарно несовместные.
,… и попарно несовместные.
По 3ей аксиоме: 
7)  где
где  -попарно несовместные события.
-попарно несовместные события.
По 3ей аксиоме: 
8)  1⊂
1⊂  2⊂
2⊂  3 …;
3 …;  =
=  = ∪
= ∪  i
i 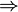 P (
P ( ) =
) =  , где P (
, где P ( ) = 1 – P(B)
) = 1 – P(B)
 =
=  (1 – P(Bn)) =1 -
(1 – P(Bn)) =1 -  P(Bn)
P(Bn)
Вывод: P(B) =  P(Bn)
P(Bn)
Поиск по сайту: