 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Неравенство Чебышева
Пусть на некотором вероятностном пространстве 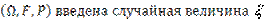 , причем
, причем
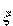 - неотрицательная.
- неотрицательная.
Лемма (Неравенство Маркова)
Для любого t>0 и любой неотрицательной случайной величины 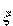 справедливо неравенство:
справедливо неравенство:
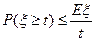
Доказательство.
Рассмотрим  {где
{где  }
} 


 , где
, где  .
.
Следствия:
1)  ,
,  - четная,
- четная,  и
и  не убывает на
не убывает на  . Тогда для любого
. Тогда для любого 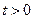
 .
.
Доказательство (следствия 1).
 .
.
2) Существует  . Тогда для любого
. Тогда для любого 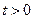
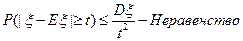
 .
.
{Из 1-го следствия, рассматривая  , получаем неравенство Чебышева}
, получаем неравенство Чебышева}
Различные виды сходимостей случайных величин
Пусть на некотором вероятностном пространстве 
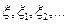
Поиск по сайту: