За наявності випадкових неконтрольованих факторів

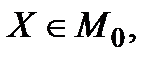
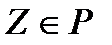Нехай у досліджуваній операції неконтрольовані фактори – це випадкові величини, тобто критерій ефективності можна записати у вигляді , де ; закон розподілу відомий точно або . Стратегією оперуючої сторони у цьому випадку буде функція .

Факт фіксації випадковості неконтрольованих факторів вважається деякою інформацією, яка повинна дати кращі результати, ніж

. (2.9)

Але якщо критерій ефективності залишається тим самим, і не міняється поняття гарантії, то ніякого нового гарантованого результату інформація щодо закону розподілу не дає. Дійсно, значення , яке реалізує (2.9), залишається можливим (хоча у деяких випадках малоймовірним). Опишемо можливості використання наявної інформації про закони розподілу для покращення оцінки (2.9).

І. Множина заміняється на меншу множину так, щоб ймовірність , де значення досить мале. Прийнятність значення 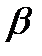обговорюється у кожному конкретному випадку. Отже, застосовується принцип гарантованого результату, але 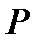у (2.9) заміняється на , а гарантію треба розуміти у сенсі малої ймовірності виходу за межі . Така імовірнісна гарантія має сенс тільки тоді, коли операція повторюється (що не завжди має місце). Крім того, у ряді випадків (при порівняно рівномірних законах розподілу) виграш від заміни на буде малим разом з при малих . Навпаки, у випадках з яскраво вираженою нерівномірністю закону розподілу виграш може бути значним.

ІІ. Зміна критерію ефективності. Такі зміни дослідник зазвичай сам робити не повинен.

Потреба у зміні критерію ефективності може виникнути, коли оцінка (2.9) дає неприйнятні результати, і немає іншої стратегії, яка б давала досить задовільні результати за формулою (2.9). Такий стан речей особливо часто зустрічається при критерії «якісного» типу, якщо оцінка ефективності стратегії, знайдена за (2.9), дорівнює 0. Тоді оперуючи сторона повинна або відмовитись від проведення операції, або змінити критерій ефективності, усунувши категоричність, властиву цілям «якісного» типу.

Поширеним підходом до зміни критерію є осереднення його за випадковостями. Вибір такого критерію пов'язаний з певним ризиком, але при багатократному повторенні операції такий ризик вважається допустимим.

У загальному випадку, коли серед неконтрольованих факторів є незалежні випадкові величини , тобто і вектор невизначених факторів , новий критерій має вигляд

, (2.10)

де − закон розподілу величини . При новому критерії оцінка ефективності має вигляд

. (2.11)

Варто зауважити, що завжди справджується нерівність

.

Права частина цієї нерівності може трактуватись як гарантована оцінка критерію (2.10) при невідомих , , які можуть бути, зокрема, довільними ступінчастими функціями.

Таким чином, збільшення інформованості про випадкові неконтрольовані фактори (закони їх розподілу) призводить до певного збільшення очікуваної ефективності, але при новому трактуванні критерію ефективності.

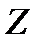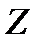У формулах (2.10), (2.11) використано незалежність векторів і . Якщо ж це не так, наприклад, противник, від якого залежить значення вектора , знає реалізацію , то замість (2.10)−(2.11) потрібно використовувати оцінку

, (2.12)

у якій порівняно з (2.10)−(2.11) змінена послідовність дій осереднення і знаходження мінімуму.

Ці дії зазвичай не перестановочні, і значення, знайдене за формулою (2.12), завжди не більше за значення, знайдене з використанням (2.10)−(2.11). Ця обставина є частковий випадок принципу 9 пункту 1.3 про роль інформованості, але у стосовно розумного противника, мета якого протилежна до мети оперуючої сторони.

Приклад 2.4. Проілюструємо запровадження нового критерію ефективності згідно з (2.10) на прикладі моделі 1.2.4. Якщо взяти критерій (1.8) і закони розподілу незалежних величин у вигляді , то застосування (2.10) до (1.8) дасть ймовірність невиходу системи з ладу

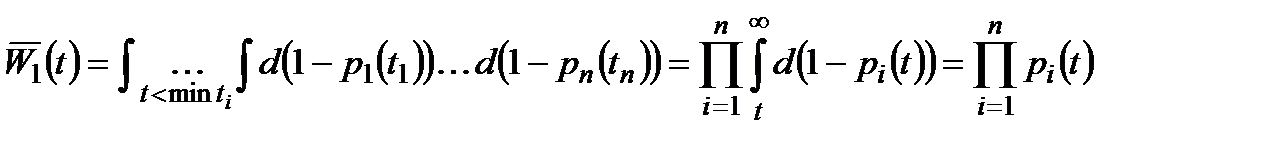. (2.13)

Замість (1.9) матимемо

.

Але, з іншого боку, законом розподілу величини , яка задається формулою (1.9), є . Звідси одержимо

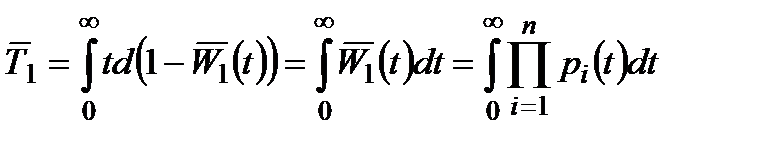. (2.14)

Формули (2.13) і (2.14) стосуються недубльованої системи. Замість (1.10) і (1.11) матимемо

; . (2.15)

Від критерію (1.15) перейдемо до

, (2.16)

а від (1.14) − до рекурентної формули

(2.17)

де − критерій при -кратному дублюванні, , .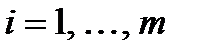

Осереднений критерій (1.14) за умови (1.16) і сам критерій (1.16) для поагрегатного паралельного з'єднання має вигляд

; . (2.18)

Нарешті, для «холодного» резервування агрегатів маємо

; (2.19)

Тут − ймовірність невиходу з ладу штук агрегатів -го типу, які вмикаються послідовно один за одним, після виходу з ладу попереднього.

Замість (1.19) матимемо

. (2.20)

Варто також відзначити, що середній час роботи разів дубльованого «холодним» способом агрегату -го типу буде

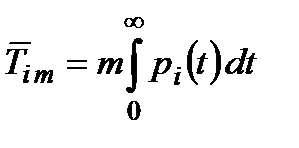. (2.21)

Формули (2.13)−(2.21) ─ основні формули теорії надійності, причому (2.15) −(2.20) є оцінками ефективності різних стратегій дублювання A−D моделі 1.2.4.

Приклад 2.5. Нехай , 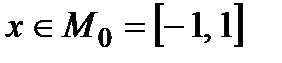; − стратегія противника, інтереси якого протилежні інтересам оперуючої сторони, , 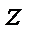− випадкова величина, рівномірно розподілена на проміжку . Знайти оцінку ефективності стратегії , якщо:

а) противник не знає реалізації ;

в) противник знає реалізацію .

Р о з в ' я з а н н я. . У випадку а), застосовуючи формулу (2.10), маємо

,

тому ;

в) при ,

при .

Застосовуючи формулу (2.12), маємо

.

Якщо досліджувана стратегія не залежить від випадкових факторів, а невизначені фактори у моделі відсутні, тоді після осереднення (2.10) одержимо модель операції без випадкових і невизначених факторів. Тоді задача оцінки ефективності стає просто обчислювальною задачею знаходження величини (2.10). У інших випадках знаходження ефективності може викликати значні труднощі. Це пояснюється двома обставинами: можливою складністю залежності стратегії від неконтрольованих факторів, а також наявністю невизначених факторів і пов'язаною з цим необхідністю знаходження мінімуму (2.11) чи (2.1) або ще складніших розрахунків згідно з (2.12).

Тому важко дати будь-які загальні рекомендації щодо методики оцінки ефективності стратегій без аналізу конкретних моделей, за винятком вказівки про можливість застосування чисельних методів знаходження інтегралів і мінімумів.

Припустимо тепер, що всі неконтрольовані фактори досліджуваної операції є випадковими. Якщо при цьому осереднення (2.10) вважається доцільним, то для його реалізації потрібно знати закони розподілу відповідних випадкових факторів. Якщо ці закони відомі недостатньо точно, тоді виникають нові невизначені фактори, а з ними і необхідність відповідних гарантованих оцінок.

Можна розрізняти три види інформованості про закон розподілу випадкової величини :

1) відомий досить точно − випадок бажаний, але зустрічається порівняно рідко, особливо при дослідження нових питань, що типово для дослідження операцій;

2) відомий тип закону розподілу, тобто функція , але невідомі або недостатньо точно відомі значення елементів вектора параметрів (наприклад, для нормального закону розподілу невідома дисперсія). У загальному випадку інформація про може бути записана у вигляді нерівності , де вектори 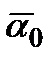, відомі.

Саме цього випадку стосується і подання невизначеної величини у вигляді випадкової, але з невизначеним законом розподілу. Дійсно, вигляд закону розподілу тут відомий:

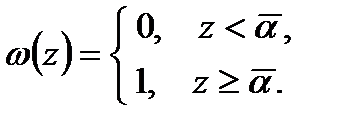
Але параметр не відомий, а обмеженій нерівностями вказаного типу або вигляду , де − деяка задана множина;

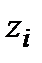3) невідомий тип закону розподілу, але відома або обмежена скінченна кількість його характеристик. Такими характеристиками можуть бути або значення у деяких точках або моменти закону розподілу

Обмеження невизначеності про закон розподілу 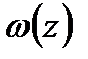мають тут такий вигляд: − неспадна функція,

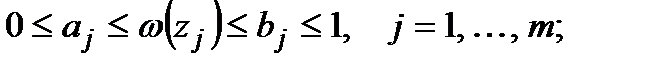
(2.22)

До наведених обмежень можна також додати такі умови: при 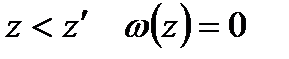або при 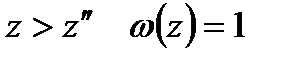та інші аналогічні умови, які обмежують область можливих значень

Об'єднуючи всі ці види інформації про закон розподілу, у загальному випадку можна записати такі нерівності

(2.23)

де − відомі функції, зокрема при 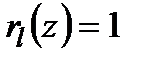для і для інших 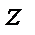одержимо першу групу умов (2.22).

Таким чином, у моделях з випадковими факторами доводиться мати справу з різною інформованістю про закони розподілу, і ця обставина істотно ускладнює оцінку ефективності стратегій і приводить до появи невизначених факторів.

Тому доцільно розглядати три типи задач оцінки ефективності, які зводяться до знаходження

(2.24)

де функції , які мають обмеження за інформацією вказаних типів.

Крім того, варто зауважити, що часто бувають відомі не моменти , а центровані моменти, наприклад, відомий не момент 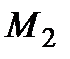, а дисперсія . Якщо центровані моменти відомі точно, то точно відомі й моменти , і задача оцінки ефективності не міняється. Але якщо, наприклад, і 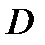тільки обмежені, то задачу оцінки ефективності спочатку можна спочатку розглядати як задачу з точно відомим і обмеженим (разом з 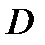), а потім розглядати задачу мінімізації за можливими значеннями . Можлива, звичайно й інша постановка задачі, але тоді область значень і не може розглядатись як прямий добуток відповідних областей значень, що ускладнить задачу оцінки ефективності, не міняючи її суті.

Вигляд закону розподілу може бути відомим або із довготривалого масового експерименту, що, наприклад, для нових взірців техніки зазвичай неможливо, або із загальних математичних і фізичних міркувань. Дуже часто при малій кількості експериментальних даних немає достатніх підстав для фіксації вигляду закону розподілу, а тим більше для його повної фіксації. Тому особливо важливою є третя постановка задачі з обмеженнями типу (2.22) або (2.23).

Зауважимо, що зазвичай вектор в має невелику кількість елементів, і тому оцінка ефективності (2.24) за умови зводиться до порівняно нескладної задачі знаходження мінімуму при малій кількості змінних.

Перейдемо тепер до детальнішого розгляду основної задачі з обмеженнями типу (2.23). Оскільки є фіксована стратегія, ефективність якої оцінюється, то можна, нехтуючи вказівкою про проміжні залежності, записати задачу знаходження гарантованої оцінки у вигляді

(2.25)

за умови, що − неспадна функція,

(2.26)

Серед умов (2.26) є й умови

Якщо області можливих значень всіх − скінченні відрізки , то , 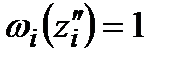; при цьому якщо кусково-неперервні та обмежені, а 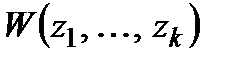неперервна то 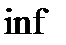можна замінити на мінімум.

Розглянемо задачу (2.25)-(2.26) у випадку :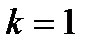

(2.27)

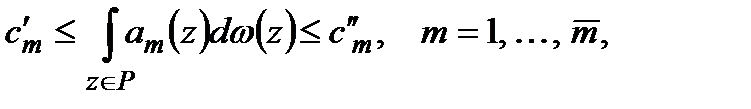(2.28)

де , − неспадна функція, а одна з умов вигляду (2.28) − це умова

.

Перетворимо цю задачу у дискретну, розбивши відрізок 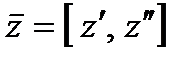на частин точками . Позначимо через приріст , розуміючи під лівосторонню границю. Очевидно, що .

Якщо функції 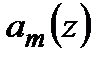обмежені і мають тільки скінченну кількість розривів першого роду, а неперервна, то,, використовуючи властивості інтеграла Стілтьєса, задачу (2.27)−(2.28) наближено можна записати у вигляді

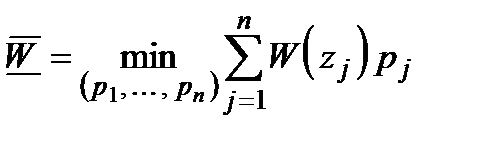(2.29)

за умов

, (2.30)

одна з яких має вигляд .

Це і є типова задача лінійного програмування. Характерним для неї є значне перевищення кількості невідомих над кількістю обмежень. Це стає очевидним при досить великих 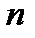, бажаних для досить точного відображення заданої варіаційної задачі (2.27)-(2.28) з неперервною змінною .

При розв'язуванні задачі (2.29)−(2.30) у випадку великих корисною є наступна теорема.

Теорема 2.1 [1]. Нехай задано таку задачу лінійного програмування: знайти найменше значення функції за умов , Тоді якщо існує розв'язок цієї задачі, і множина розв'язків обмежена, то існує і такий розв'язок, для якого не більше, ніж з змінних 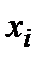відмінні від 0.

Зауважимо, що внаслідок 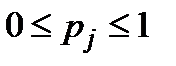множина розв'язків (2.29)-(2.30) обмежена.

Переходячи до границі при і враховуючи обмеженість , можна одержати наступну теорему.

Теорема 2.2 [1]. Якщо значення належать обмеженому інтервалу, а і неперервні, то задача оцінки ефективності при невизначеному законі розподілу , обмеженому нерівностями типу (2.28), має дискретний розв'язок, а саме, такий розв'язок, що кількість точок , що мають ненульову ймовірність, не перевищує .

Якщо значення належить необмеженому інтервалу або якщо і 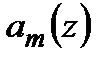кусково-неперервні, для розв'язування задачі (2.27)−(2.28) може бути використана

Теорема 2.3. Нижню грань ефективності при невизначеному , обмеженому умовами (2.28) можна одержати як нижню грань ефективності при дискретному 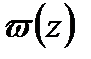, що має не більше, ніж точок з ненульовими ймовірностями.

Використання теорем 2.2, 2.3 є зручним, оскільки для оцінки ефективності потрібно знати лише сам мінімум, а не закон розподілу, при якому цей мінімум досягається; отже, достатньо знати хоча б одну реалізацію мінімуму і, звичайно, бажано у певному розумінні найпростішу. Саме цю можливість надає теорема 2.2.

Відзначимо випадок, коли . Тоді кількість точок з ненульовими ймовірностями повинно бути не більша, ніж , але й не менша, оскільки інакше неможливо задовольнити рівності 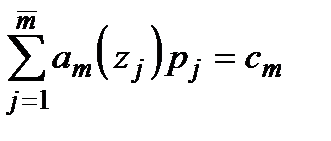. Але тоді або визначається однозначно при фіксованих , або ця система взагалі не має розв'язку. Таким чином, визначивши, , зведемо варіаційну задачу (2.27)−(2.28) до задачі пошуку мінімуму функції змінних .

Приклад 2.6. Нехай контрольований фактор , випадковий неконтрольований фактор . Про функцію розподілу відомо лише, що . Знайти оцінку ефективності довільної стратегії-константи, якщо критерій ефективності задано функцією .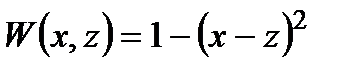

Р о з в ' я з а н н я. Знаходимо спочатку осереднений критерій ефективності

.

Тепер потрібно знайти

при таких умовах щодо закону розподілу

.

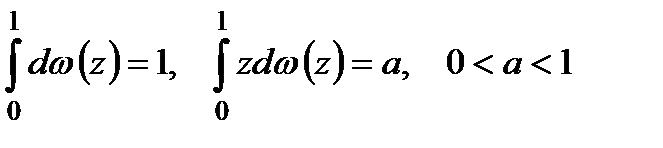Оскільки маємо дві рівності-обмеження, то за теоремою 2.2. розв'язок задачі оцінки ефективності будемо шукати серед законів розподілу вигляду

Звідси випливає, що можливі два випадки:

а) . Тоді ;

в) Тоді , ,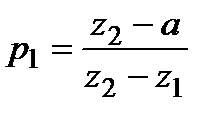

Позначимо . Зауважимо, що . Тому

,

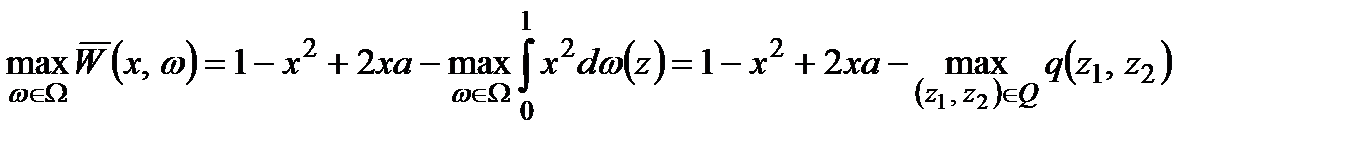де

.

Далі маємо: тобто єдина стаціонарна точка знаходиться на межі області .

Розглянемо поведінку функції на межі області .

1) ;

2)

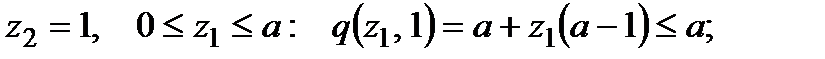
3)

4) .

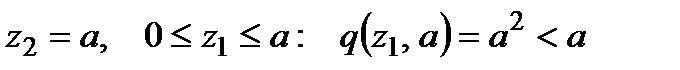Отже, , .

Міркування щодо розв'язування задачі (2.25)−(2.26) як неперервної задачі лінійного програмування при наведені у [1]. Але практичну ефективність застосування чисельних методів лінійного програмування має лише при порівняно невеликих 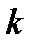і .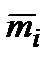

Отже, оцінка ефективності стратегій у загальному випадку є порівняно нескладною задачею, якщо закони розподілу випадкових факторів відомі досить точно і, крім випадкових факторів, інші неконтрольовані фактори відсутні.

Якщо у операції є різні типи неконтрольованих факторів, то оцінка ефективності стратегії визначається у залежності від додаткових припущень про ці фактори. Нехай, наприклад, у операції неконтрольований фактор 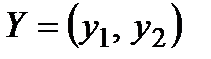, , де вибирається першим противником, який знає реалізацію випадкової величини , що має невизначеність у законі розподілу, а − другим противником, який не знає цієї реалізації. Тоді, якщо інтереси противників невідомі, а оперуюча сторона дозволяє осереднення за випадковостями, то оцінка ефективності стратегії має вигляд

.

Приклад 2.7. Розв'язати задачу з прикладу 2.5, якщо − випадкова величина з невизначеністю у законі розподілу:

.

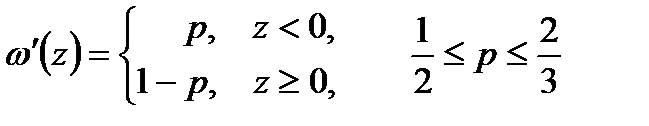Р о з в ' я з а н н я.

а) у даному випадку ефективність стратегії оцінюємо за формулою

,

Враховуючи, що , маємо

,

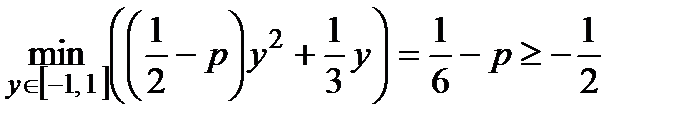Тому ;

в) використовуючи формулу

,

одержимо

,

отже, .

Поиск по сайту: