Узагальнена схема операції та її нормальної математичної моделі

ОСНОВНІ ПОНЯТТЯ І ОЗНАЧЕННЯ ДОСЛІДЖЕННЯ ОПЕРАЦІЙ.

Операція – це сукупність дій, об'єднаних єдиним задумом і спрямованих на досягнення певної мети. Поки не задано мету, операція не існує. У даній операції мета єдина.

Сукупність осіб або автоматів, дії яких спрямовані на досягнення мети даної операції, називають оперуючою стороною. Виокремлення оперуючої сторони має сенс, тому що в операції можуть бути задіяні особи або природні сили, які не прагнуть досягнення мети даної операції. Наприклад, у футбольному матчі, крім гравців команди, тренерів і уболівальників, які входять до оперуючої сторони, є також активні противники, які прагнуть завадити досягненню мети, та судді, які мають бути нейтральними щодо досягнення мети операції.

Оперуюча сторона є, взагалі кажучи, дещо невизначений конгломерат учасників, що грають різні ролі у досягненні мети операції. У деяких випадках до її складу увійдуть ті учасники, які визначають мету операції. В інших випадках мета операції призначається ззовні (наприклад, у так званих ієрархічних системах, у яких складники вищого рівня визначають мету складників нижчого рівня). Але, якщо трактувати оперуючу сторону досить широко та включити до неї всі складники ієрархічної системи, тоді можна вважати, що оперуюча сторона сама собі формує мету операції.

Дослідник операції належить до оперуючої сторони і переслідує ту ж саму мету. Ця мета повинна бути йому відома, так само, як і обставини проведення операції. Але у реальних ситуаціях ступінь інформованості дослідника про операцію може бути іншим, ніж ступінь інформованості оперуючої сторони. Тому дослідник має право на деякі припущення та спрощення.

Дослідник операції зазвичай сам не приймає рішень з вибору способів дій, а лише допомагає у цьому оперуючій стороні. Отже, незважаючи на приналежність дослідника до оперуючої сторони, він виконує особливу роль, досліджуючи операцію в цілому, але часто не маючи всієї повноти інформації про операцію і не приймаючи кінцевих рішень.

Виокремлення дослідника операцій в самостійну частину оперуючої сторони доцільне, оскільки дає змогу чіткіше з'ясувати деякі питання взаємодії при постановці задач дослідження операцій та при прийнятті рішень.

Для досягнення мети оперуючи сторона має у своєму розпорядженні деякий запас (ресурс) активних засобів, використовуючи і, як правило, витрачаючи які, вона може досягати мети.

Наприклад, при розв'язуванні виробничих задач до активних засобів відносять запаси сировини, наявне обладнання, робочу силу, гроші.

Способи дій, тобто способи використання активних засобів, називаються стратегіями оперуючої сторони. Оцінка прийнятності і порівняння стратегій оперуючої сторони і є суттю роботи дослідника операцій.

Результати операції з досягнення певної мети при даній кількості активних засобів залежать від вибору стратегій, тобто від факторів, що знаходяться у розпорядженні оперуючої сторони (контрольованих факторів).

Але результати можуть залежать і від факторів, які не контролюються оперуючою стороною. Такі фактори утворюють обстановку проведення операції. Зокрема, у сільському господарстві неконтрольованим фактором є погодні умови; при стрільбі − так зване розсіювання снарядів; у військових діях і спортивних змаганнях –дії противника, який намагається завадити оперуючій стороні.

Найзагальніший якісний опис компонент будь-якої операції закінчується вказівкою на інформованість оперуючої сторони і дослідника операцій про обстановку проведення операції, тобто про точність знання значень неконтрольованих факторів у даній конкретній операції. Крім того, важливою є також інформованість різних частин оперуючої сторони про рішення, дії і результати дій цих частин.

Математична модель операції повинна давати, нехай наближено, кількісний опис операції; тому математичний еквівалент повинен мати всі перелічені компоненти операції.

Як і всякий процес, хід операції повинен описуватись деякою кількістю 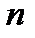фазових координат ; вважається, що задавання функцій дає змогу повністю описувати конкретний перебіг операції у даній моделі. Чим більше фазових координат, тим, взагалі кажучи, точнішим є опис операції, але й тим складніше дослідження моделі.

Як правило, хід операції з точки зору досягнення мети можна характеризувати невеликою кількістю або навіть одною фазовою координатою.

Ступінь відповідності перебігу операції поставленій меті характеризується значенням функціоналу 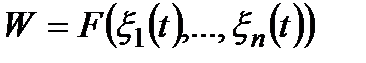, який називається критерієм ефективності; мета операції зводиться до прагнення збільшити (або зменшити) значення критерію ефективності. Надалі вважатимемо, що метою є збільшення значення критерію.

Отже, прагнення збільшення критерію ефективності є математичним описом мети операції. У даній моделі він повністю заміняє собою мету, і дослідник має справу тільки з ним.

Так само, як і мета, її еквівалент – критерій ефективності – у моделі операції єдиний і може бути вибраний (за узгодженням з оперуючою стороною) довільно у тій мірі, як і сама мета.

Приклади критеріїв ефективності:

1) різниця забитих і пропущених м'ячів у футбольному матчі;

2) кількість виготовленої продукції на виробництві;

3) значення 0 або 1 в операції посадки на поїзд.

Зауважимо, що критерій ефективності не слід плутати з фазовими координатами. Зокрема, різниця забитих і пропущених м'ячів у футбольному матчі – фазова координата , але не обов'язково критерій. Критерієм може бути 1 або 0 в залежності від виграшу або невиграшу, тобто критерій може бути задано у такий спосіб

Незнання або недостатньо точне знання критерію ефективності – це прямий наслідок недостатньо чіткого розуміння мети операції або недостатніх знань про процес її перебігу. Таке незнання може звести нанівець дослідження операції або її проведення.

Активні засоби характеризуються своєю кількістю. Якщо активні засоби мають різну природу, то їх кількість описується вектором , а обмеженість активних засобів математично виражається як обмеженість компонент вектора: , .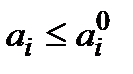

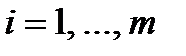Можливості активних дій оперуючої сторони можна подати як набір деяких величин , що впливають на фазові координати. Ці величини можуть бути довільно вибрані оперуючою стороною з деякої заданої множини. Взагалі кажучи, цей вибір міняється в часі або з отриманням інформації про перебіг операції, тобто про фазові координати. Величини можна трактувати як реальне розбиття активних засобів на групи, які використовуються в різних місцях і в різний час, або просто як номер того чи іншого способу використання активних засобів. Другий випадок застосовується частіше, коли способів дій скінченна кількість.

Стратегією оперуючої сторони з точки зору дослідника операції є у загальному випадку правило поведінки, яке дозволено очікуваною інформацією, тобто оператори , де , а – затримка у часі, необхідна для отримання і обробки інформації про перебіг операції та реалізацію рішення про призначення в момент . Це можливо за умови наявності у оперуючої сторони інформації про , яка дає можливість реалізації операторів. Якщо ж така інформація не очікується, то вибір не може залежати від відповідних 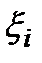, і набір самих є стратегією. Допустимі за інформованістю та іншими міркуваннями стратегії оперуючої сторони утворюють множину, яку часто називають простором стратегій.

У свою чергу залежать від значень 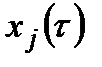, вектора і деякої кількості неконтрольованих оперуючою стороною функцій , які відображають обстановку, що змінюється у часі.

Неконтрольовані фактори, враховуючи інформованість про них дослідника, можна розділити на три групи.

I. Фіксовані фактори, значення яких відомі досліднику операції.

II. Випадкові фіксовані фактори, тобто випадкові процеси з відомими законами розподілу.

III. Невизначені фактори, для яких відома тільки область розподілу факторів, в якій вони можуть знаходитись, або область, в якій знаходяться закони розподілу, якщо відомо, що фактор випадковий, але закон розподілу точно не відомий. У останньому випадку краще говорити про невизначений закон розподілу випадкового фактора.

Невизначені фактори, в свою чергу, можна розбити на такі підгрупи:

а) невизначені фактори, які з'являються при наявності діючих незалежно від оперуючої сторони осіб або автоматів, не зацікавлених, взагалі кажучи, у досягненні мети оперуючої сторони; невизначені фактори такого типу можна умовно назвати стратегіями противника, що має свої активні засоби, обмеження яких і набір (простір) стратегій противника утворюють область подібних факторів;

б) невизначені фактори, причиною появи яких є недостатність знань про деякі процеси і величини; такі невизначеності можна назвати природними;

в) невизначені фактори, що відображають нечіткість знання мети операції або критерію ефективності; формально цей тип невизначених факторів, звичайно, можна віднести до природних, але необхідно підкреслити його особливе місце в дослідженні операцій.

Найбільш яскраві приклади невизначеностей першого типу дають військові дії і спорт, де наперед невідома тактика противника створює невизначеності, що суттєво впливають на результат операції. Систематичним вивченням ситуацій з невизначеностями такого типу займається теорія ігор.

Прикладом невизначеності другого типу є невизначеність у законі розподілу випадкової величини, для якої відомі тільки математичне сподівання і дисперсія.

Нарешті, прикладом невизначеності третього типу є невизначеність у законі виборі критерію оцінки діяльності виробничих підприємств, що виробляють продукцію декількох різних типів.

Зауважимо, що наведене розбиття неконтрольованих факторів зроблено з точки зору дослідника операцій і відповідає його інформованості у момент проведення досліджень.

Як вже зазначалось, оперуюча сторона в цілому може мати більше інформації, що відображається у понятті стратегії. Невизначені та випадкові фактори або відповідні їм значення фазових координат можуть стати відомими (фіксованими факторами) під час проведення операції або навіть дещо раніше (але після проведення досліджень), і ця інформація може бути використана при виборі способу поведінки.

Сформульована загальна схема моделі операції недостатньо наочна і вимагає систематичного використання функціонального аналізу. Відповідні методики дослідження операції розроблені недостатньо.

Тому надалі обмежимось дискретною моделлю, яку можна розглядати як наближення наведеної моделі. Багато практичних задач є дискретними моделями.

У дискретній моделі вважається, що перебіг операції повністю характеризується значеннями фазових координат у дискретні моменти часу; ці значення можна записати у вигляді , де – номер моменту часу. Так само рішення про вибір приймається дискретно, тому їх значення можуть бути перенумеровані у вигляді ; неконтрольовані фактори відповідно записуються у вигляді 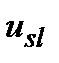. При цьому є функціями всіх і (і, звичайно, вектора ) при .

Стратегією відповідно буде набір функцій , де , а − затримка.

Для подальшого спрощення запису узагальненої схеми моделі позначимо через вектор і через вектор . Вектор і вектор – це значення, яких можуть набувати стратегії у момент або у всі моменти. Саму стратегію позначатимемо через . Зокрема, коли додаткова інформація про не очікується, стратегія зводиться до вибору значень наперед (під час досліджень), тобто . Але якщо інформація про очікується і передбачається її використання, то множина досліджуваних стратегій буде ширшою.

Зауваження.

А. Неконтрольовані фіксовані фактори сталі уданій моделі, тому у функції, яка виражає критерій, вказівкою на залежність від таких факторів можна знехтувати.

В. Для зручності замість одного вектора можна вживати іноді окремі позначення для різних типів неконтрольованих факторів, наприклад, , , де 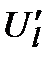означає випадкові неконтрольовані фактори, − природні невизначеності (включаючи і третій тип) і − невизначені фактори, пов’язані з розумним противником; вектор активних засобів такого противника позначатимемо через .

С. Оскільки є функціями контрольованих і неконтрольованих факторів, в узагальненій схемі моделі можна, нехтуючи вказівкою про проміжну залежність від , записати критерій ефективності у вигляді

(1.1)

Цей запис і стане загальною спрощеною схемою моделі, якщо буде зазначено, що оперуючи сторона прагне збільшувати 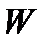і що можливі значення векторів , , 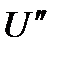знаходяться у відповідних областях, що відомі досліднику операції, а для відомі закони розподілу. Крім того, досліднику операції повинно бути задана множина досліджуваних стратегій, тобто вектор-функцій , де і 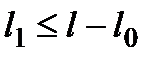, , , які дають змогу вибору оперуючою стороною векторів за наявності інформації про попередні значення контрольованих і неконтрольованих факторів.[*]

З цього запису випливає, що при відсутності випадкових і невизначених неконтрольованих факторів достатньо розглядати стратегії типу (стратегії-константи). У цьому випадку інформованість оперуючої сторони про неконтрольовані фактори (а, отже, і про ) не перевищує інформованості дослідника операції.

Оскільки задавання стратегії 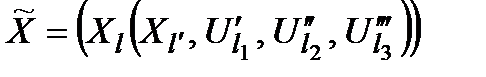при даних значеннях неконтрольованих факторів визначає , то цим визначається і значення 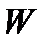. Таким чином, крім запису (1.1), можна користуватись і записом

,

де .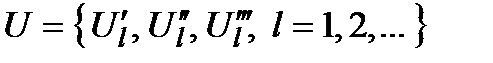

Для перебігу операції наявність інформації про значення фазових координат у всі моменти, що передують моменту , еквівалентна наявності інформації про значення всіх контрольованих і неконтрольованих факторів у ці моменти. Ця обставина, несуттєва з точки зору узагальненої схеми моделі, досить важлива з практичної точки зору, особливо при дослідженні операцій з наявністю противника.

Оскільки і у даній моделі зазвичай фіксовані, у записі (1.1) будемо нехтувати вказівкою про залежність від цих ці аргументів.

Надалі для зручності будемо вживати також такі позначення:

− множина всіх можливих значень контрольованих факторів ;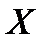

− неконтрольовані фактори, для яких відома тільки область N їх значень;

− випадкові фактори: досліднику операцій відома множина значень випадкової величини 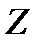; крім того, закон розподілу цієї випадкової величини або відомий точно, або відомо лише, що , де 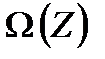− деяка множина законів розподілу (випадкова величина з невідомим законом розподілу);

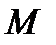− множина досліджуваних стратегій оперуючої сторони.

Як вже було зазначено, на момент проведення операції оперуюча сторона може бути більше інформованою про неконтрольвані фактори, ніж дослідник операції під час проведення дослідження. Інформація, яку буде мати оперуюча сторона на момент проведення операції, фіксується у моделі інформаційною гіпотезою. Якщо оперуюча сторона не має додаткової інформації про неконтрольовані фактори, то її стратегіями є самі контрольовані фактори з М ₀. Якщо неконтрольвані фактори стануть відомі оперуючій стороні на момент проведення операції, то її стратегіями є всеможливі відображення ; множину всіх таких відображень позначатимемо . Інформаційну гіпотезу можна задати за допомогою інформаційної функції , визначеної на множині ; оперуючій стороні на момент проведення операції стане відоме значення . Множиною стратегій оперуючої сторони у цьому випадку є множина

.

Інформаційну гіпотезу можна задати й іншими способами. У будь-якому випадку множина стратегій М є підмножиною .

Враховуючи наведені позначення, критерій ефективності можна записати у вигляді , де функція визначена на множині . Його можна також довизначити на множині : .

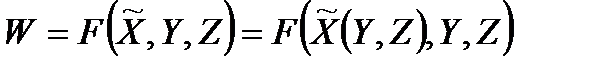Якщо , , то критерій ефективності можна записати у вигляді матриці

.

Стратегії оперуючої сторони у цьому випадку можна задати вектором .

Якщо множина значень інформаційної функції скінченна, складається з різних елементів і , то множина складається з стратегій.

Приклад 1.1. Нехай , ,

,

інформаційну функцію задано у такий спосіб: 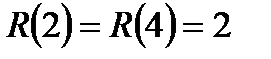. Тоді множина стратегій складається з 9 стратегій:

, , ,

, , ,

, , .

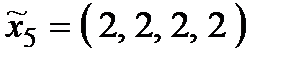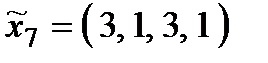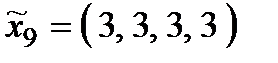Критерій ефективності, довизначений на множині , має вигляд:

1.2. Приклади моделей операцій

Наведемо декілька прикладів моделей операцій, що свідчать про різноманітність можливих практичних варіантів моделей.

Поиск по сайту: