АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Критерій Севіджа

Читайте также:
  1. І. Статистичні гіпотези. Статистичний критерій перевірки нульової гіпотези.
  2. Критерій Гурвіца.
  3. Критерій Дарбіна — Уотсона
  4. Критерій згоди Колмогорова
  5. Критерій згоди Романовського
  6. Критерій згоди Ястремського
  7. Критерій фон Неймана
  8. Перевірка гіпотези про закон розподілу. Критерій згоди Пірсона.
  9. Перевірка гіпотези про нормальний закон розподілу генеральної сукупності. Критерій узгодженості Пірсона

Критерій Вальда є настільки песимістичним, що іноді може приводити до нелогічних висновків. Нехай критерій відображає втрати оперуючої сторони у деякій операції і має вигляд

Застосування критерію Вальда приводить до висновку про оптимальність другої стратегії оперуючої сторони. Але інтуїтивно є бажання вибрати першу стратегію, оскільки можливим залишається другий стан природи, при якому втрати становлять лише 90 одиниць, у той час, як застосування другої стратегії завжди приводить до втрат у 10000 одиниць.

Критерій Севіджа «виправляє» цей недолік, розглядаючи нову матрицю, елементи якої обчислюються як різниця між результатом, що забезпечується даною стратегією при заданому стані природи і найкращим можливим результатом у тих самих умовах:

.

По суті, виражає «жаль» особи, яка приймає рішення, з приводу того, що не вибрано найкращу дію в умовах . Застосування принципу гарантованого результату при аналізі матриці дає наступне правило для визначення оптимальної стратегії:

.

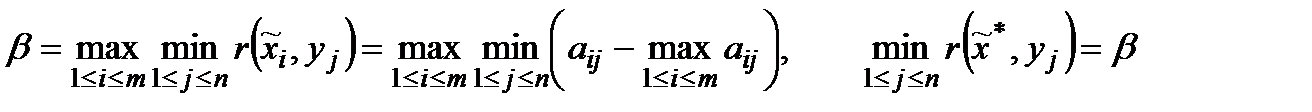Повертаючись до наведеного вище прикладу, одержимо:

,

,

і оптимальною вважатимемо першу стратегію.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)