ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА

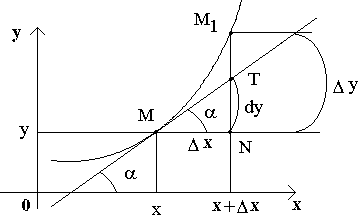Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δ x, тогда функция получит приращение Δ y = NM ₁. Значениям x +Δ x и y +Δ y на кривой y = f(x) будет соответствовать точка

M ₁(x +Δ x; y +Δ y).

Из Δ MNT находим NT = MN ·tg α. Т.к. tg α = f '(x), а MN = Δ x, то NT = f '(x)·Δ x. Но по определению дифференциала dy = f '(x)·Δ x, поэтому dy = NT.

Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.

ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ДИФФЕРЕНЦИАЛА

Ранее мы видели, что если u является независимой переменной, то дифференциал функции y = f '(u) имеет вид dy = f '(u) du.

Покажем, что эта форма сохраняется и в том случае, когда u является не независимой переменной, а функцией, т.е. найдем выражение для дифференциала сложной функции. Пусть y=f(u), u=g(x) или y = f(g(x)). Тогда по правилу дифференцирования сложной функции:

.

Следовательно, по определению

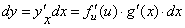, но g '(x) dx = du, поэтому dy= f'(u)du.

Мы доказали следующую теорему.

Теорема. Дифференциал сложной функции y=f(u), для которой u=g(x), имеет тот же вид dy=f'(u)du, какой он имел бы, если бы промежуточный аргумент u был независимой переменной.

Иначе говоря, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство дифференциала называется инвариантностью формы дифференциала.

Пример. . Найти dy.

Учитывая свойство инвариантности дифференциала, находим

.

Поиск по сайту: