ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ

Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.

Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у ₀ имеет производную g '(v₀), отличную от нуля, то в соответствующей точке x₀ = g (x₀) функция y=f(x) имеет производную f '(x₀), равную 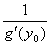, т.е. справедлива формула .

Доказательство. Т.к. x=g(y) дифференцируема в точке y₀, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x₀ = g (y₀). Следовательно, при Δ x →0 Δ y →0.

Покажем, что .

Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δ y →0. Тогда Δ x →0 и α(Δx)→0, т.е. .

Следовательно,

,

что и требовалось доказать.

Эту формулу можно записать в виде .

Рассмотрим применение этой теоремы на примерах.

Поиск по сайту: