Примеры. 1. Составить уравнения касательной и нормали к графику функции у = tg2x в точке с абсциссой x0=π/4

1. Составить уравнения касательной и нормали к графику функции у = tg² x в точке с абсциссой x₀ =π/4.

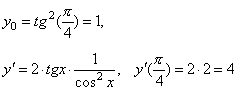
Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4 x – π + 1.

Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4· x + π/16 + 1.

2. Составить уравнения касательной и нормали к графику функции у = 0.5·(x – 2)² + 5 в точке M (2; 5).

y '= x – 2, y '(2) = 0. Следовательно, касательная параллельна оси Ox, а значит ее уравнение y = 5. Тогда нормаль параллельна оси Oy и имеет уравнение x = 2.

3. Найти уравнение касательной и нормали к эллипсу 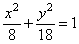в точке M (2; 3).

Найдем y ' по правилу дифференцирования неявной функции .

Уравнение касательной: 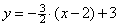,т.е. .

Уравнение нормали: 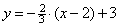, т.е. .

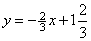4. Составить уравнения касательной и нормали к циклоиде x = t – sin t, y = 1 – cos t в точке М (x ₀; y ₀), которая соответствует значению параметра t = π/2.

При t =π/2 x ₀= π/2 – 1, y ₀=1.

.

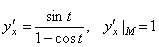Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2.

Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.

Поиск по сайту: