Примеры. 1. Функция y=sin x, определенная при -∞<x<+∞, является ограниченной, так как при всех значениях x |sin x|≤1 = M

1. Функция y =sin x, определенная при -∞< x <+∞, является ограниченной, так как при всех значениях x |sin x |≤1 = M.

2. Функция y =x²+2 ограничена, например, на отрезке [0, 3], так как при всех x из этого отрезка |f(x)| ≤f (3) = 11.

3. Рассмотрим функцию y =ln x при x Î (0; 1). Эта функция неограниченна на указанном отрезке, так как при x →0 ln x →-∞.

Функция y=f(x) называется ограниченной при x → a, если существует окрестность с центром в точке а, в которой функция ограничена.

Функция y=f(x) называется ограниченной при x→∞, если найдется такое число N> 0, что при всех значениях х, удовлетворяющих неравенству |x|>N, функция f(x) ограничена.

Установим связь между ограниченной функцией и функцией, имеющей предел.

Теорема 1. Если и b – конечное число, то функция f(x) ограничена при x→a.

Доказательство. Т.к. , то при любом ε>0 найдется такое число δ>0, что при вех значениях х, удовлетворяющих неравенству |x-a|< δ, выполняется неравенство |f(x) –b|< ε. Воспользовавшись свойством модуля |f(x) – b|≥|f(x)| - |b|, последнее неравенство запишем в виде |f(x)|<|b|+ ε. Таким образом, если положить M=|b|+ ε, то при x→a |f(x)|<M.

Замечание. Из определения ограниченной функции следует, что если , то она является неограниченной. Однако обратное неверно: неограниченная функция может не быть бесконечно большой. Приведите пример.

Теорема 2. Если 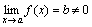, то функция y=1/f(x) ограничена при x→a.

Доказательство. Из условия теоремы следует, что при произвольном ε>0 в некоторой окрестности точки a имеем |f(x) – b|< ε. Т.к. |f(x) – b|=|b – f(x)| ≥|b| - |f(x)|, то |b| - |f(x)|< ε. Следовательно, |f(x)|>|b| - ε >0. Поэтому и .

Поиск по сайту: