ПОНЯТИЕ ДИФФЕРЕНЦИАЛА ФУНКЦИИ. СВЯЗЬ МЕЖДУ ДИФФЕРЕНЦИАЛОМ И ПРОИЗВОДНОЙ

Пусть функция y=f(x) дифференцируема на отрезке [ a; b ]. Производная этой функции в некоторой точке х ₀ Î [ a; b ] определяется равенством

.

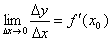Следовательно, по свойству предела

Умножая все члены полученного равенства на Δ x, получим:

Δ y = f ' (x ₀)·Δ x + a·Δ x.

Итак, бесконечно малое приращение Δ y дифференцируемой функции y=f(x) может быть представлено в виде суммы двух слагаемых, из которых первое есть (при f ' (х ₀) ≠ 0) главная часть приращения, линейная относительно Δ x, а второе – бесконечно малая величина более высокого порядка, чем Δ x. Главную часть приращения функции, т.е. f ' (х ₀)·Δ x называют дифференциалом функции в точке х ₀ и обозначают через dy.

Таким образом, если функция y=f(x) имеет производную f ' (x) в точке x, то произведение производной f ' (x) на приращение Δ x аргумента называют дифференциалом функции и обозначают:

Найдем дифференциал функции y= x. В этом случае y ' = (x)' = 1 и, следовательно, dy = dx =Δ x. Таким образом, дифференциал dx независимой переменной x совпадает с ее приращением Δ x. Поэтому формулу (1) мы можем записать так:

Но из этого соотношения следует, что . Следовательно, производную f '(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.

Ранее мы показали, что из дифференцируемости функции в точке следует существование дифференциала в этой точке.

Справедливо и обратное утверждение.

Если для данного значения x приращение функции Δ y = f (x +Δ x) – f(x) можно представить в виде Δ y = A ·Δ x + α, где α – бесконечно малая величина, удовлетворяющая условию , т.е. если для функции y=f(x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f '(x)= А.

Действительно, имеем , и так как при Δ x →0, то .

Таким образом, между дифференцируемостью функции и существованием дифференциала имеется очень тесная связь, оба понятия равносильны.

Примеры. Найти дифференциалы функций:

1.

2. .

Поиск по сайту: