 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Во многих приложениях математического анализа встречаются комбинации показательных функций. Эти комбинации рассматриваются как новые функции и обозначаются:
– гиперболический синус.
– гиперболический косинус.
С помощью этих функций можно определить еще две функции.
– гиперболический тангенс.
– гиперболический котангенс.
Функции sh x, ch x, th x определены, очевидно, для всех значений x, т.е. их область определения (–∞; +∞). Функция же cthx определена всюду за исключением точки x = 0.
Между гиперболическими функциями существуют следующие соотношения, аналогичные соответствующим соотношениям между тригонометрическими функциями.
Найдем: 
.
Т.е. 
.
.
Итак, 
.
Следовательно, 
.
Найдем производные гиперболических функций
.
Аналогично можно показать 
.
.
Т.е. 
и 
.
Графики гиперболических функций. Для того чтобы изобразить графики функций
shx и chx нужно вспомнить графики функций y = ex и y = e-x
Проведем исследования функции y = th x.
1.
a. D(f) = (–∞; +∞), точек разрыва нет.
b. Точка пересечения с осями координат 
.
2.
, функция возрастает на (–∞; +∞).
3. 
4.
a. Вертикальной асимптоты нет.
b. 
.
y = cth x
1. D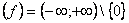 
. Точка разрыва x = 0 cth x = 0 – нет
2.
убывает на 
.
3. 
4.
a. 
b. При x → +∞
Поиск по сайту: