Примеры. 1. Найти производную четвертого порядка функции y= ln x

1. Найти производную четвертого порядка функции y = ln x.

.

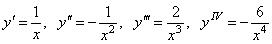2. .

3. Найти производную n -го порядка функции y = e^{k x} .

y '= k ·e^kx, y ''= k ²·e^kx, y ''' = k ³·e^kx, …, y ⁽ⁿ⁾ = k ⁿ·e^kx.

4. Найти производную n -го порядка функции y = sin x.

Имеем

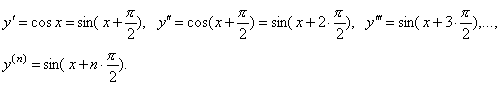
Выясним механический смысл второй производной. (Механический смысл первой производной – скорость).

Пусть материальная точка движется прямолинейно по закону s =s(t), где s – путь, проходимый точкой за время t. Тогда скорость v этого движения есть v= s'(t) = v(t), т.е. тоже некоторая функция времени.

В момент времени t скорость имеет значение v=v(t). Рассмотрим другой момент времени t +Δ t. Ему соответствует значение скорости v ₁ = v (t +Δ t). Следовательно, приращению времени Δ t соответствует приращение скорости Δ v = v ₁ – v = v (t + Δ t) – v (t). Отношение называется средним ускорением за промежуток времени Δ t.

Ускорением в данный момент времени t называется предел среднего ускорения при Δ t →0:

.

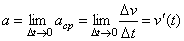Таким образом, ускорение прямолинейного движения точки есть производная скорости по времени. Но как мы уже видели, скорость есть производная пути s по времени t: v = s '. Учитывая это, имеем:

a = v '(t) = (s ')' = s ''(t),

т.е. ускорение прямолинейного движения точки равно 2-й производной пути по времени

a = S''(t).

ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

Пусть имеем функцию y=f(x), где x – независимая переменная. Тогда дифференциал этой функции dy = f '(x) dx также зависит от переменной x, причем от x зависит только первый сомножитель f '(x), а dx = Δ x от x не зависит (приращение в данной точке x можно выбирать независимо от этой точки). Рассматривая dy как функцию x, мы можем найти дифференциал этой функции.

Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d ² y: d (dy)= d ² y.

Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому

d ² y = d (dy) = d [ f '(x) dx)] = [ f '(x) dx ]' dx = f ''(x) dx·dx = f ''(x)(dx)².

Принято записывать (dx)² = dx ². Итак, d ² у = f ''(x)d x ².

Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:

d ³ y = d (d ² y)=[ f ''(x) dx ²]' dx = f '''(x) dx ³.

Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: d ⁿ(y)= d (d ^n-1 y)

Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:

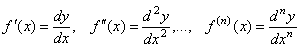
Поиск по сайту: