 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
РАЗЛОЖЕНИЕ ПО ФОРМУЛЕ МАКЛОРЕНА НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. Рассмотрим функцию f(x)=ex. Представим ее по формуле МакЛорена в виде суммы многочлена и некоторого остатка. Для этого найдем производные до (n +1) порядка:
Таким образом, получаем
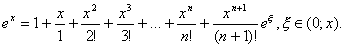
Используя эту формулу и придавая x различные значения, мы сможем вычислить значение ex.
Например, при x =1, ограничиваясь n =8, получим формулу, позволяющую найти приближенное значение числа e:
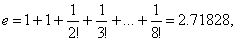причем остаток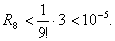 
Отметим, что для любого x R остаточный член 
Действительно, так как ξ (0; x), то величина e ξ ограничена при фиксированном x. При x > 0 e ξ < ex. Докажем, что при фиксированном x 
Имеем 
Если x зафиксировано, то существует натуральное число N такое, что | x |< N.
Обозначим 
Заметив, что 0<q<1, при n>N можем написать
Но 
, не зависящая от n, а 
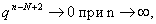так как q<1. Поэтому 
Следовательно, 
Таким образом, при любом x, взяв достаточное число слагаемых, мы можем вычислить ex с любой степенью точности.
2. Выпишем разложение по формуле МакЛорена для функции f(x) =sin x.
Найдем последовательные производные от функции f(x) =sin x.
Подставляя полученные значения в формулу МакЛорена, получим разложение:
Несложно заметить, что преобразовав n -й член ряда, получим
.
Так как 
, то аналогично разложению ex можно показать, что 
для всех x.
Пример. Применим полученную формулу для приближенного вычисления sin 20°. При n =3 будем иметь:
Оценим сделанную погрешность, которая равна остаточному члену:
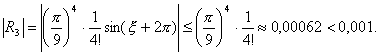
Таким образом, sin 20°= 0,342 с точностью до 0,001.
3. f(x) = cos x. Аналогично предыдущему разложению можно вывести следующую формулу:
Здесь также 
для всех x. Докажите формулу самостоятельно.
4. f(x) =ln (1+ x). Заметим, что область определения этой функции D(y) =(–1; +∞).
Найдем формулу МакЛорена для данной функции.
Подставим все найденные производные в ряд МакЛорена.
Можно доказать, что если x (–1;1],то 
, т.е. выведенная формула справедлива при x (–1;1].
5. f(x) = (1+ x)m, где m R, m≠0.
При m≠Z данная функция определена при x> –1. Найдем формулу МакЛорена для этой функции:
И следовательно,
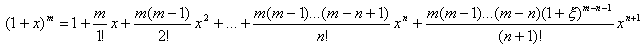Можно показать, что при | x |<1 
Поиск по сайту: