ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ

Пусть y = f(u), а u = u (x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.

Областью определения функции y = f(u(x)) является либо вся область определения функции u = u (x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y = f(u).

Операция "функция от функции" может проводиться не один раз, а любое число раз.

Установим правило дифференцирования сложной функции.

Теорема. Если функция u = u (x) имеет в некоторой точке x₀ производную 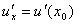и принимает в этой точке значение u₀ = u (x₀), а функция y= f(u) имеет в точке u₀ производную y '_u= f '(u₀), то сложная функция y = f(u(x)) в указанной точке x₀ тоже имеет производную, которая равна y '_x= f '(u₀)· u '(x₀), где вместо u должно быть подставлено выражение u = u (x).

Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.

Доказательство. При фиксированном значении х ₀ будем иметь u ₀= u (x ₀), у ₀ =f(u ₀ ). Для нового значения аргумента x₀ +Δ x:

Δ u = u (x₀ + Δ x) – u (x ₀), Δ y = f (u₀ +Δ u) – f (u₀).

Т.к. u – дифференцируема в точке x₀, то u – непрерывна в этой точке. Поэтому при Δ x →0 Δ u →0. Аналогично при Δ u →0 Δ y →0.

По условию 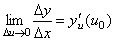. Из этого соотношения, пользуясь определением предела, получаем (при Δ u →0)

,

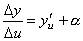где α→0 при Δ u →0, а, следовательно, и при Δ x →0.

Перепишем это равенство в виде:

Δ y = y '_uΔ u +α·Δ u.

Полученное равенство справедливо и при Δ u =0 при произвольном α, так как оно превращается в тождество 0=0. При Δ u =0 будем полагать α=0. Разделим все члены полученного равенства на Δ x

.

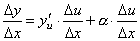По условию 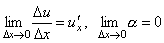. Поэтому, переходя к пределу при Δ x →0, получим y '_x= y '_u·u '_x. Теорема доказана.

Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной.

Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y '_x осуществляется последовательным применением предыдущей теоремы.

По доказанному правилу имеем y '_x= y '_u· u '_x. Применяя эту же теорему для u '_x получаем , т.е.

y '_x = y '_x· u '_v· v '_x = f '_u (u)· u '_v (v)· v '_x (x).

Поиск по сайту: