 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.
Рассмотрим функцию y=f(x) непрерывную на отрезке [ a, b ]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.
Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[ a, b ]:
1. Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
2. Вычислить значения функции на концах отрезка при x = a, x = b.
3. Из всех полученных значений выбрать наибольшее и наименьшее.
Примеры.
1. Найти наибольшее и наименьшее значения функции  на отрезке [–2; –0,5].
на отрезке [–2; –0,5].
Найдем критические точки функции. 
Вычислим значения функции в найденной точке и на концах заданного отрезка.

Итак, 
2. Найти наибольшее и наименьшее значения функции y=x -2·ln x на [1; e].

3. Чему равна наименьшая площадь боковой поверхности прямого кругового конуса объема 3π?
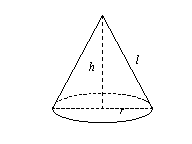

По теореме Пифагора
 .
.
Следовательно,  .
.
 .
.
Найдем критические точки функции S: S ' = 0, т.е. 
Покажем, что при найденном значении h функция Sбок достигает минимума.

 .
.
4.
 Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.
Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.
Пусть r – радиус основания цилиндра, h – высота.
Нам нужно максимизировать объем цилиндра  .
.
Используя условие задачи, найдем связь между r и h. По теореме Пифагора из треугольника ABC следует, что  . Отсюда
. Отсюда  .
.
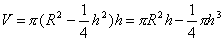 , по смыслу задачи 0≤ h ≤2 R.
, по смыслу задачи 0≤ h ≤2 R.
 .
.
Покажем, что при найденном значении h функция V принимает наибольшее значение.


афик функции y = f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y = f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Примеры.
1. Полуокружность  выпукла на [–1; 1].
2. Парабола y = x2 вогнута на интервале (-∞; +∞).
3. График функции в одних интервалах может быть выпуклым, а в других вогнутым. Так график функции y = sin x на [0,2; π ], выпуклый в интервале (0; π) и вогнутый в (π; 2 π).
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y = f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f ''(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение выпукла на [–1; 1].
2. Парабола y = x2 вогнута на интервале (-∞; +∞).
3. График функции в одних интервалах может быть выпуклым, а в других вогнутым. Так график функции y = sin x на [0,2; π ], выпуклый в интервале (0; π) и вогнутый в (π; 2 π).
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y = f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f ''(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение  . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
|   
|
Итак, уравнение кривой имеет вид y = f(x). Обозначим  ординату касательной, соответствующую абсциссе x. Тогда
ординату касательной, соответствующую абсциссе x. Тогда  . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет
. Следовательно, разность ординат кривой и касательной при одном и том же значении x будет  .
.
Разность f(x) – f(x0) преобразуем по теореме Лагранжа  , где c между x и x0.
, где c между x и x0.
Таким образом,
 .
.
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа:  , где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
, где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
1. Предположим, что x > x 0. Тогда x0 < c1 < c < x, следовательно,  (x – x 0) > 0 и (c – x 0) > 0. Поэтому
(x – x 0) > 0 и (c – x 0) > 0. Поэтому  .
.
2. Пусть x < x0, следовательно, x < c < c 1 < x 0 и (x – x 0) < 0, (c – x 0) < 0. Поэтому вновь  .
.
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
1. Установить интервалы выпуклости и вогнутости кривой y = 2 – x2.
Найдем y '' и определим, где вторая производная положительна и где отрицательна. y ' = –2 x, y '' = –2 < 0 на (–∞; +∞), следовательно, функция всюду выпукла.
2. y = ex. Так как y '' = e x > 0 при любых x, то кривая всюду вогнута.



3. y = x3. Так как y '' = 6 x, то y '' < 0 при x < 0 и y '' > 0 при x > 0. Следовательно, при x < 0 кривая выпукла, а при x > 0 вогнута.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x 0) = 0 или f ''(x 0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых.
1.  Найдем производные заданной функции до второго порядка.
Найдем производные заданной функции до второго порядка.
 . .
 . Вторая производная не существует при x = 1. Исследуем эту точку на возможный перегиб.
Итак, точка перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞; 1).
2. . Вторая производная не существует при x = 1. Исследуем эту точку на возможный перегиб.
Итак, точка перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞; 1).
2.  Возможные точки перегиба найдем, решив уравнение 2 x2 – 1 = 0. Отсюда
Возможные точки перегиба найдем, решив уравнение 2 x2 – 1 = 0. Отсюда  .
Точки перегиба .
Точки перегиба  . Функция выпукла на . Функция выпукла на 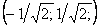 и вогнута на и вогнута на  .
3. y = ln (1 – x2). Область определения функции D(y) = (-1; 1). .
3. y = ln (1 – x2). Область определения функции D(y) = (-1; 1).
 . .
 при всех x из (–1; 1).
Следовательно, f(x) выпуклая на (–1; 1). при всех x из (–1; 1).
Следовательно, f(x) выпуклая на (–1; 1).
|    
|
Поиск по сайту: