Примеры. 2. Пусть f(x)=x2–4,g(x)=x2–5x+6 – бесконечно малые

1. Пусть f(x)=x ², g(x)= 5 x. Функции являются бесконечно малыми при x →0. Найдем . Следовательно, f(x) – бесконечно малая высшего порядка относительно g(x).

2. Пусть f(x)=x ²–4, g(x)=x ²–5 x +6 – бесконечно малые при x →2.

.

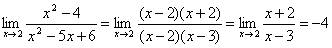Поэтому f(x) и g(x) одного порядка.

3. f(x)= tg2 x,g(x) = 2 x – бесконечно малые при х →0.

.

Следовательно, f ≈ g.

4. – бесконечно малые при n →∞.

– этот предел не существует. Поэтому говорят, что функции f и g не сравнимы.

При вычислении пределов полезно помнить о следующем свойстве эквивалентных бесконечно малых функций.

Теорема. Пусть f и g – бесконечно малые функции при х → а. Если и f ≈ f ₁, g ≈ g ₁, то , т.е. если отношение двух бесконечно малых имеет предел, то этот предел не изменится, если каждую из бесконечно малых заменить эквивалентной бесконечно малой.

Доказательство. Имеем 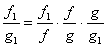. Тогда

,

что и требовалось доказать.

Докажите самостоятельно эквивалентность следующих бесконечно малых функций при

x →0: sin x ≈ x, tg x ≈ x, arcsin x ≈ x, arctg x ≈ x, 1–cos x ≈ x ²∕2,log _a (1+ x) ≈ x/ ln a, ln (1+ x) ≈ x, (1+ x)^m–1 ≈ mx,a^x –1 ≈ x ln a,e^x –1 ≈ x.

Поиск по сайту: